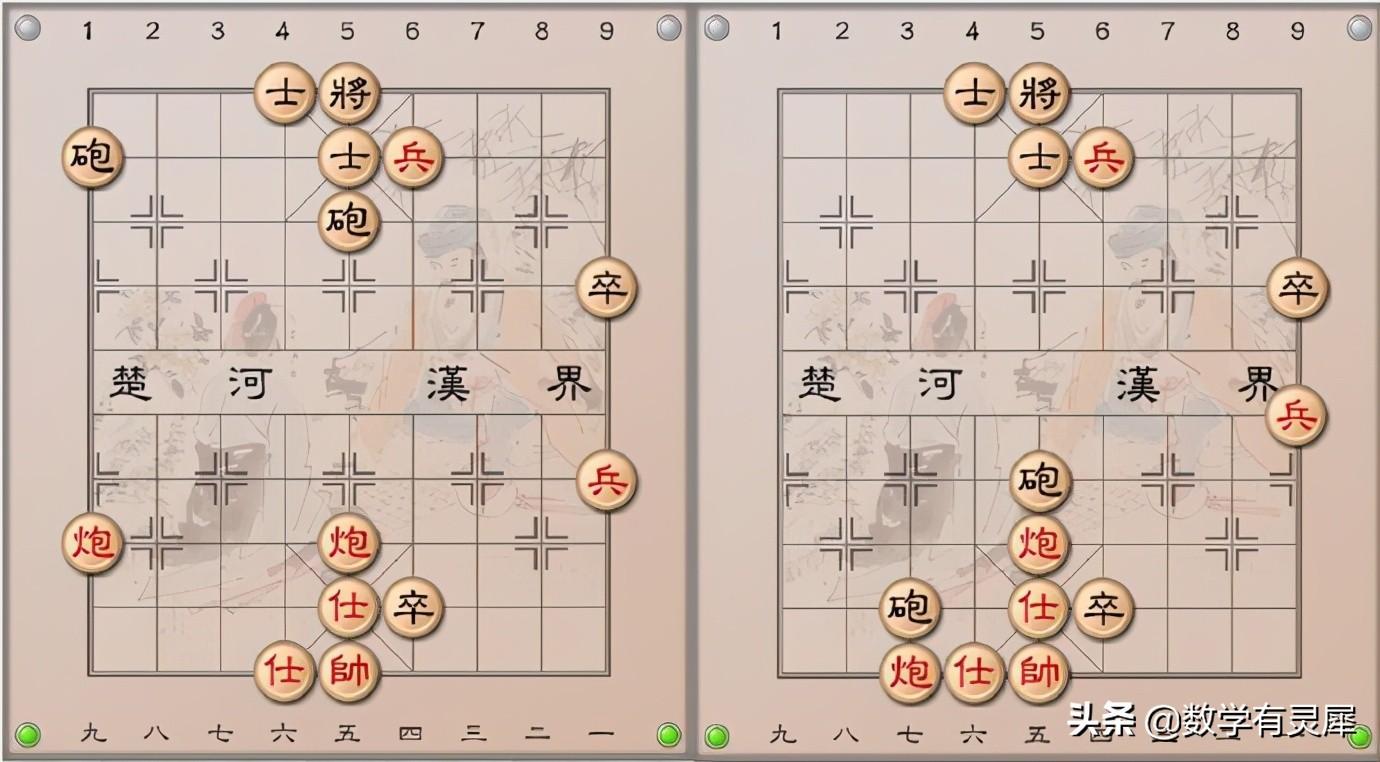
街头有时会看到上图的象棋残局,查了查它的渊源,果然搜到《杨官璘象棋研究》记载了一个类似的棋局,原来此局就是大名鼎鼎的江湖残局“盲公顶棍”,贾题韬《象棋残局新论》也介绍了两个类似的局面,看来这个残局还颇有名气。
来观察一下,双方具有对称的棋局:士与过了河的兵(卒)均不能动,否则输棋。能动的只有两个炮和一个兵(卒),且炮只能进不能平,否则会被对方闷宫杀。这局棋制胜的关键在于,一路兵卒和两路跑的空步数,谁先走完最后的空步数,谁就赢棋。大约就是玩左轮手枪一类游戏技巧吧,把最后一手之前留给自己,让对方必死。

电脑上用象棋软件计算,结果竟然发现各种棋软都没法解开这个残局。于是人工加电脑反复演练,才发现这个貌似平淡的残局没有和棋。一般都会走成某一方子力被围困,一动就输掉的棋形。
喜爱玩象棋的朋友都明白“先行之利”,尤其是残局,先走一步的优势就更明显了。有趣的是,这个残局的结果竟然是红先黑胜,换黑棋先走的结果就是红胜,这是一个注定了谁先走谁输的象棋残局。
这个棋局还有蛮多变例,通过改变炮的初始位置和对头兵的数量,残局的胜负结果也会发生变化。
反复研究后,一些似曾相识的规律越来越清晰,没错!这些规律不但能给出残局正确的解法,也能够指引出决定局面胜负的最深奥义。下面我们来描述这个棋局的数学原理:
首先必须建立数学模型,这个说容易也不容易。先来讲一个简单的游戏。把石子摆成四排,第一排1颗、第二排3颗、第三排5颗、第四排7颗(下图)。规则是这样的,两人轮流来拿石子,每次可以在同一排中拿走任意颗,至少拿走1颗,谁拿到最后一颗石子,谁就赢了。例如:我先来拿,我可以一次拿走第四排的全部7颗;或者在第二排拿走2颗,留下1颗,这都是规则允许的。但是在第二排拿1颗并且在第三排也拿1颗,这种不在同一排内拿石子的方法是违反规则的。因为石子的数量是有限的,每次拿都会造成数量减少,两人轮流拿,最后一个石子总是会被拿走。拿走最后一个石子的就是胜者。也就是说这个游戏一定能分出胜负,不会出现平局。
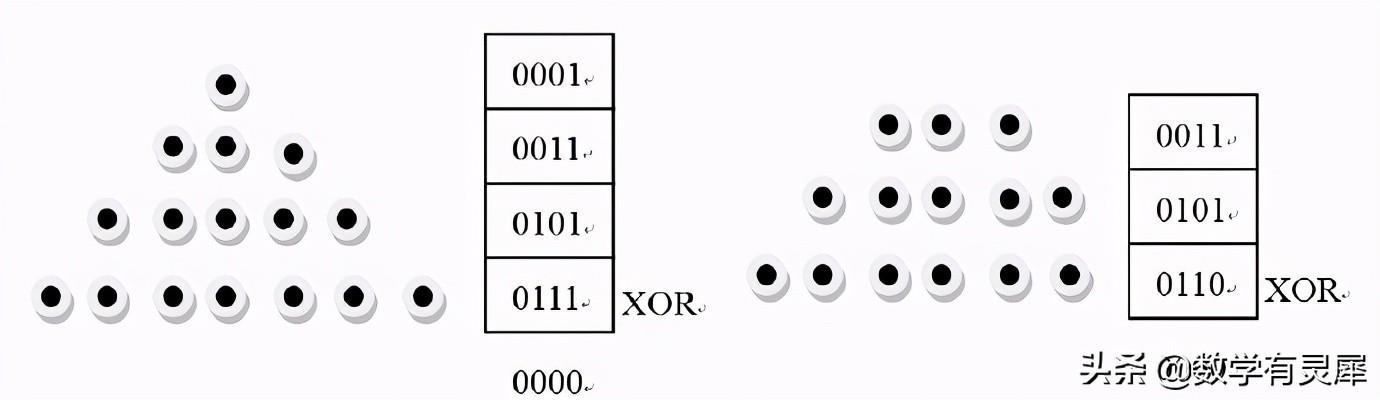
下面来说一下这个游戏的求胜方法:首先把每一排的石子数量的十进制数转化成二进制数。我们会得到0001、0011、0101、0111。然后我们对这个数连续进行XOR运算(二进制逻辑异或运算),简单理解为不进位的二进制加法运算。即0001 XOR 0011=0010,0010 XOR 0101=0111,0111 XOR 0111=0000。如果初始值为0000就注定谁先拿谁就要输了。
例如,你先拿了第4排的1颗石子。剩余石子对应的数值分别为,0001、0011、0100、0111,XOR运算的结果为0001;轮到我拿了,我就拿走第1排的1颗石子,此时剩余石子对应的数值为0011、0100、0111,XOR运算的结果为0000;这样依次类推下去,只要你拿完了,XOR运算的结果就不会是0000,我只要再拿掉一些石子,使结果恢复到0000即可。当然,对于不同的局面,使XOR运算结果恢复到0000的方法是不同的,而且也可能同时存在多种恢复方法。反复使用这种过程,就可以保证我在最后一次拿光剩余的石子,也就是我赢了。如果你看懂了,再按照上述方法演示几次,就可以掌握这个游戏的取胜之道了。

言归正传,让我们回头再看前面的象棋残局。把棋盘上一路的兵之间可走的步数看作1,把五路炮之间可走的步数看作4,把九路炮之间可走的步数看作5。转化成对应的二进制为0001、0100、0101,XOR运算结果为0000。这下明白为啥这个象棋残局注定是谁先走谁输了吧!这就是数学的魅力。
当然,象棋的走法相比于石子游戏更复杂,规则也更多。但是只要抓住它们在逻辑上的共同点,也就可以把这两个看起来毫不相关的游戏当作同一个游戏来玩了。本文到此结束,因为已经“授人以渔”,所以我不会列出破解残局的棋谱,更无必要讲述此局中繁杂的变化。
















