高中数学三角函数单调性的判断和方法汇总,考试易出错,得分点低
高中数学当中有关于三角函数单调性的。胖墩主要是以正弦函数,余弦函数的最简单形式为基础而展开的。其涉及到的求最值问题,单调区间或者是定期间上的函数。取值范围等都是以这个内容来进行展开,所以在学习的过程当中我们一定要掌握最基本函数的单调性。否则在学习复杂的三角函数时容易出现问题。

首先,对于正弦函数和余弦函数的图像性质以及单调性最值问题都要了解清楚,从图形的识别和应用当中能够提高大家对单调性和最值的认识,这也是三角函数学习过程中最基本的方法。
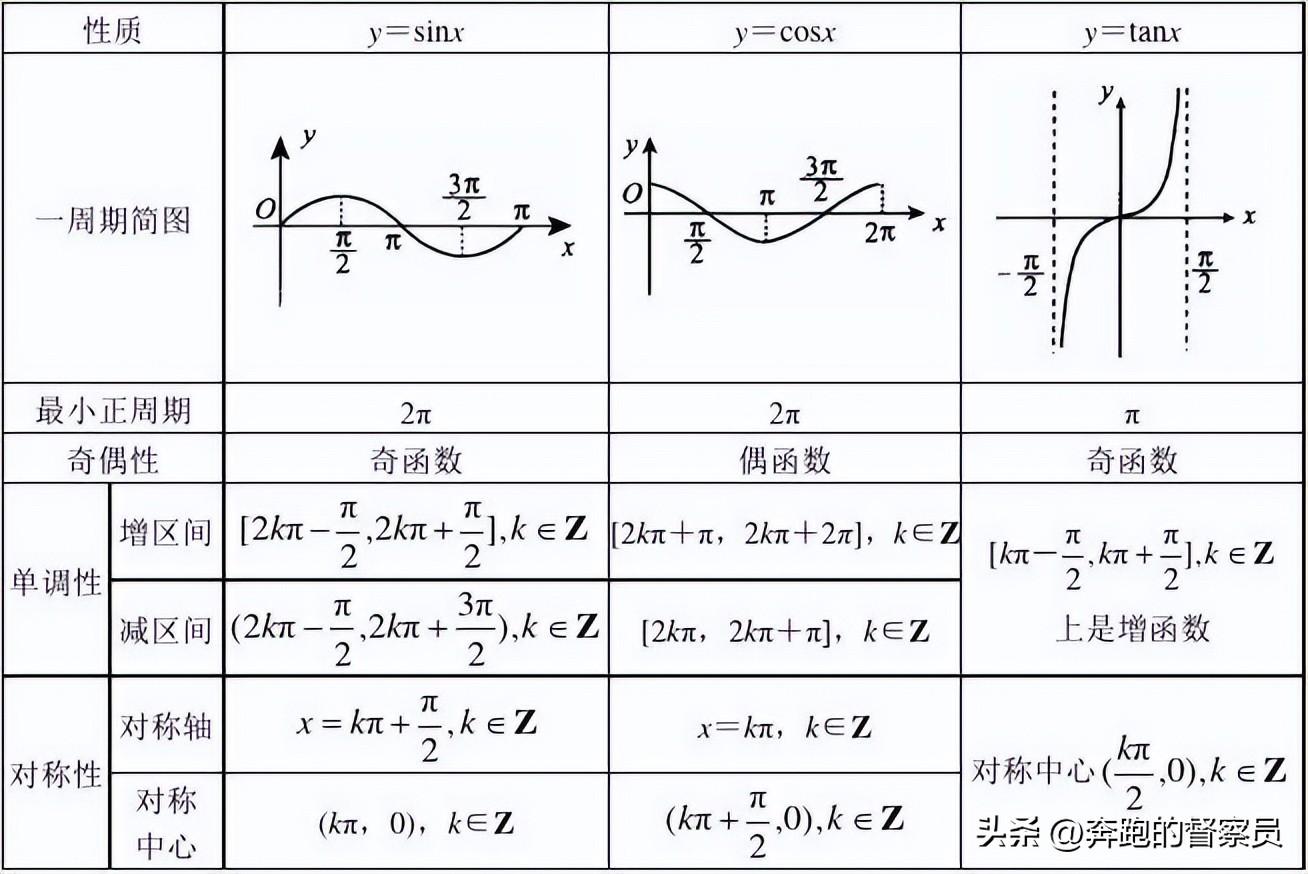
求形如函数y=Asin(ωx+φ)的单调性以及定区间上的单调区间,可以借助正弦函数,余弦函数的单调期间来进行化简,然后通过不等式的求解就可以得到其复杂函数的单调区间。这种类型的题型考察基本上可以作为大题来进行考察,所以在高考的考察过程当中,我们需要对这种类型的函数求区间问题,明确其方法以及注意的易错点,才能真正的掌握这类型题型。

其次,函数y=Asin(ωx+φ)的单调性才是重难点。
对于函数y=Asin(ωx+φ)的单调性,当ω>0时,由于内层函数u=ωx+φ是单调递增的,(也就是说我们可以将其抗作是一个复合函数。也可以将ωx+φ看作一个整体。)所以该函数的单调性和y=sin x的单调性相同,故可完全按照函数y=sin x的单调区间解决;但当ω<0时,内层函数u=ωx+φ是单调递减的,此时该函数的单调性和函数y=sinx的单调性相反,就不能再按照函数y=sinx的单调性解决,一般是根据三角函数的奇偶性将内层函数的系数变为正数后再加以解决。对于带有绝对值的三角函数应该根据图像,从直观上进行判断。

或者说换一种方式来进行理解,当w<0时,先用诱导公式将式子变形,将x的系数化为正。而当A>0,w>0时,将函数ωx+φ带入正弦或余弦函数的单调区间,可以解得与之单调性一致的单调区间。当A<0,w>0时,同样的方法可以求得与正弦函数或余弦函数单调性相反的单调区间。
在这提醒大家,如果我们采用复合函数的单调性来求解三角函数的单调性时,一定要遵循“同增异减”的规律。

函数y=Asin(ωx+φ)的单调性求解过程当中,内存函数一般为一次函数由w来决定函数的单调性,所以是比较简单的内容啊,函数的振幅的字母a的正负则决定了三角函数的外层函数的单调性。所以我们在进行单调区间求解时,一定要先盯住这两个重要的字母,再进行求解过程中的分量,那么也就掌握了判定。三角函数单调性区间的重要技巧。

写在最后,对于高中数学三角函数单调性求解的方法都是以最基础的正弦或余弦函数的单调性为基础而展开的,所以在这过程当中对于这两种函数的单调性不仅要从理论上进行掌握,而且结合图形进行观察,更能取得优势,然后拓展到最为复杂的三角函数,求解释采用。复合函数的形式或者是以正余弦函数为基础把中间的ωx+φ看作一个整体来进行求解。
















