您可能知道三个主要的三角函数——正弦、余弦和正切。您可能还知道一些额外的三角函数，称为正割、余割和余切。您可能已经看到，反三角函数有时被称为反正弦、反余弦等。

但是这些名字是从哪里来的呢？

在本文中，我们将了解这些名称的来源。

如果您不熟悉圆的弦、切线和正割，请查看圆文章的各个部分。

初级三角函数——正弦、正切、正割

当我们考虑主要的三角函数时，我们通常会想到正弦、余弦和正切。这些是最常用于解决三角函数问题的函数。

但从历史上看，正弦函数、正切函数和正割函数被认为是主要函数。

为什么是这样？如果我们在一个单位圆内形成一个三角形，中心有一个角a ，那么正弦函数、正切函数和正割函数将告诉我们三个边中每一个的长度，以a表示。每个功能都以其相关的方面命名。

正弦函数

正弦函数与圆的弦有关。弦是圆周上两点之间的线。这是一个圆的弦的例子：

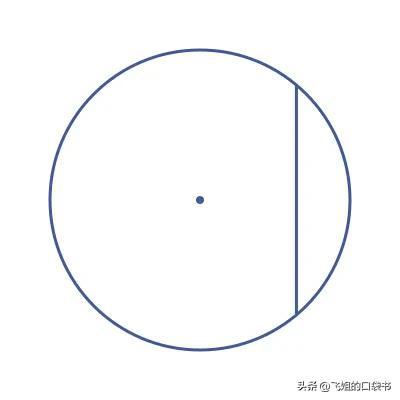
正弦这个词是圆的弦的旧术语。它起源于梵语中的弓弦（如弓箭），因为圆的弦和圆弧看起来很像弓：

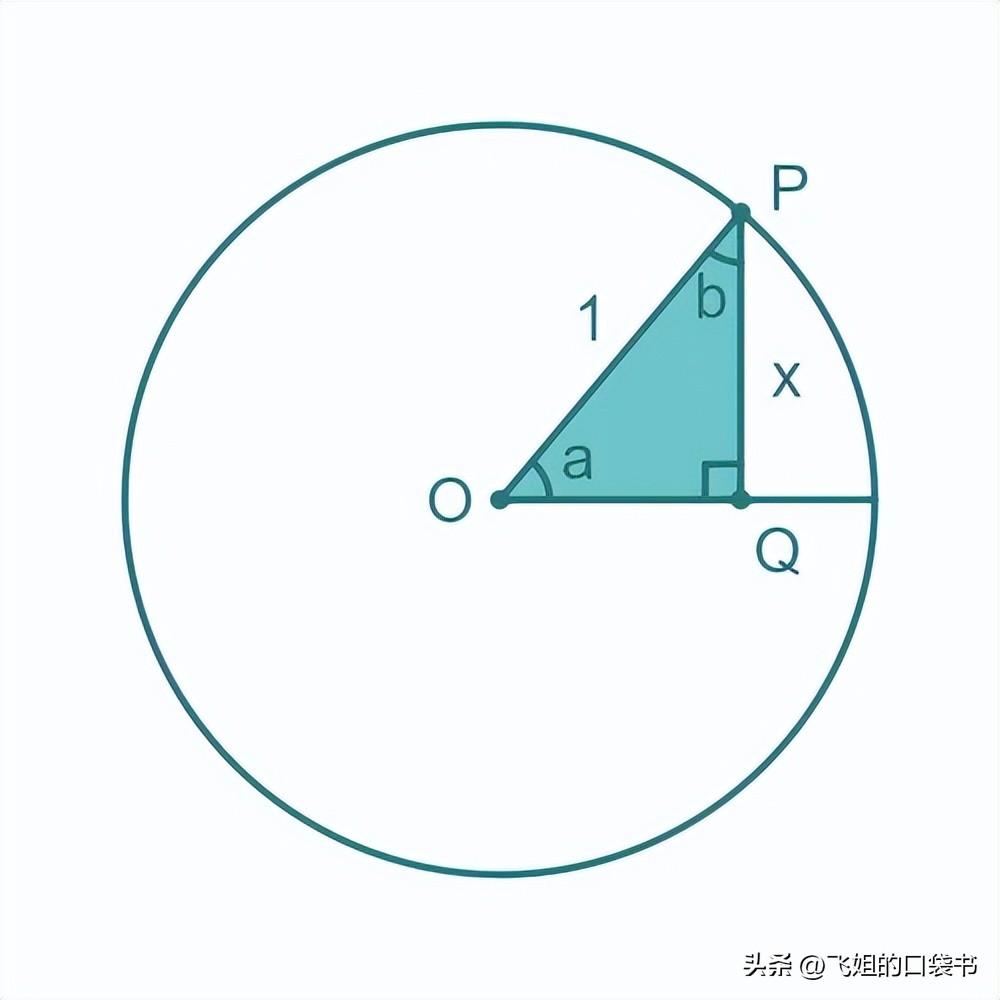
要了解正弦函数与圆的弦的关系，我们可以在单位圆内画一个三角形：

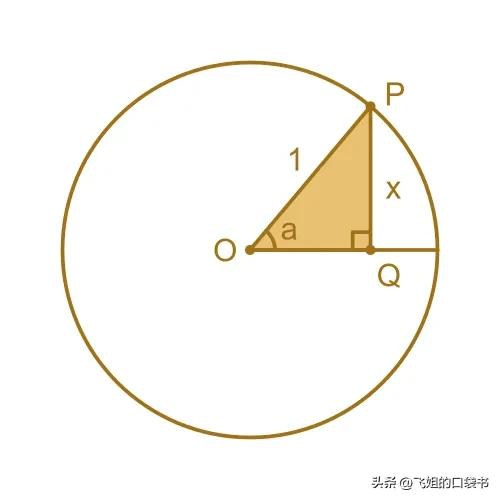
这里，直角三角形POQ在中心有一个角a 。斜边OP的长度为 1，因为它是单位圆的半径。与角a相对的一侧的长度为x。

正弦函数的定义是：

现在，如果我们绘制第二个全等三角形ROQ，我们可以看到直线PR形成圆的弦：

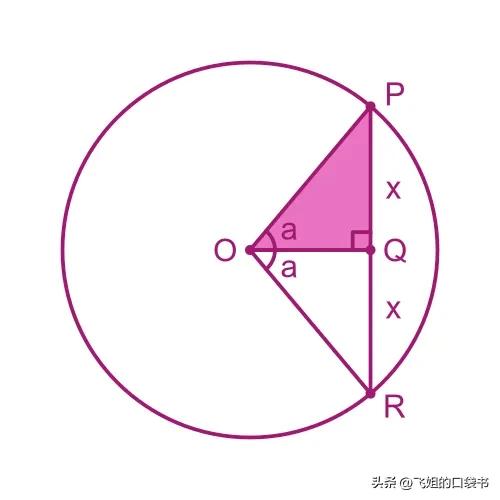
所以sin a告诉我们长度x，它是构成弦PR一部分的三角形边的长度。我们称它为正弦函数，因为正弦表示和弦。

实际上，长度x等于弦长的一半。正弦函数有时被称为半弦函数，尽管现在很少使用该术语。

正切函数

如您所料，正切函数与圆的切线有关。圆的切线是与圆的圆周相切但不与圆相交的线。这是一个例子：

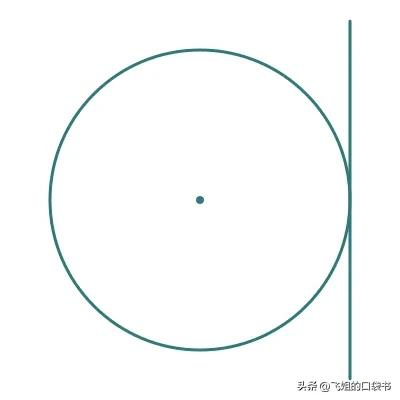
我们可以再次在单位圆内画一个三角形来发现正切函数与圆的正切的关系：

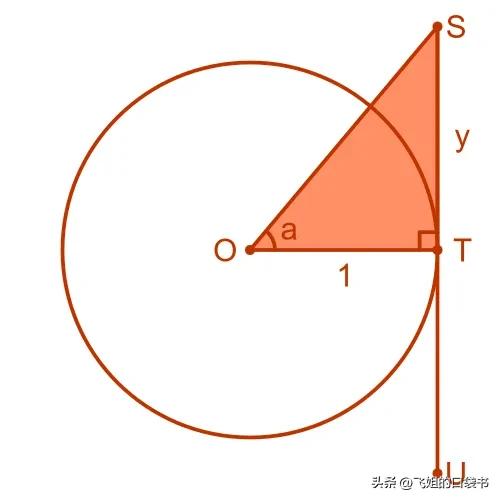
这个三角形TOS与我们为正弦函数绘制的三角形不太一样。前面的三角形有一条长度为 1 的斜边，这个三角形的边与长度为 1 的角a相邻。

对边ST的长度为y。

该图还显示了圆的切线，即直线SU。ST是该切线的一部分。

正切函数的定义是：

所以tan a告诉我们长度y。这是构成切线SU一部分的三角形ST的边长。

因此我们称它为正切函数。

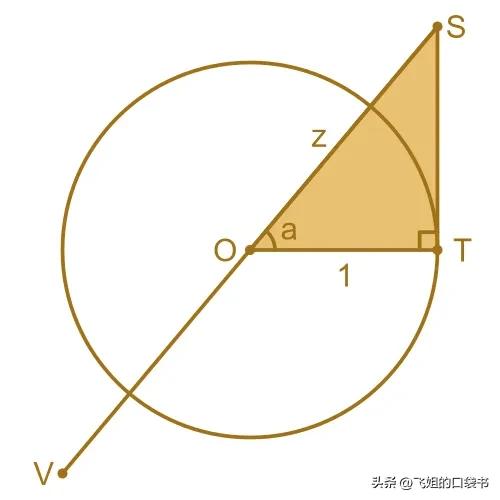
正割函数

正如您所料，正割函数与圆的正割有关。割线是在两个地方穿过圆周的线。割线类似于弦，只是它延伸到圆周之外：

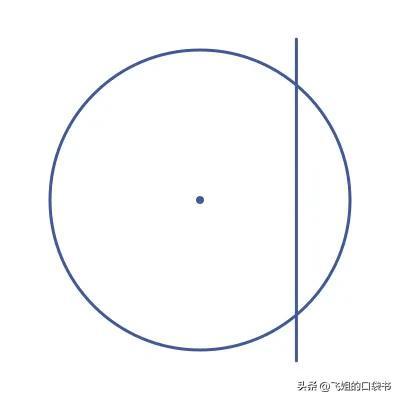
这次我们绘制与切线示例相同的三角形TOS ：

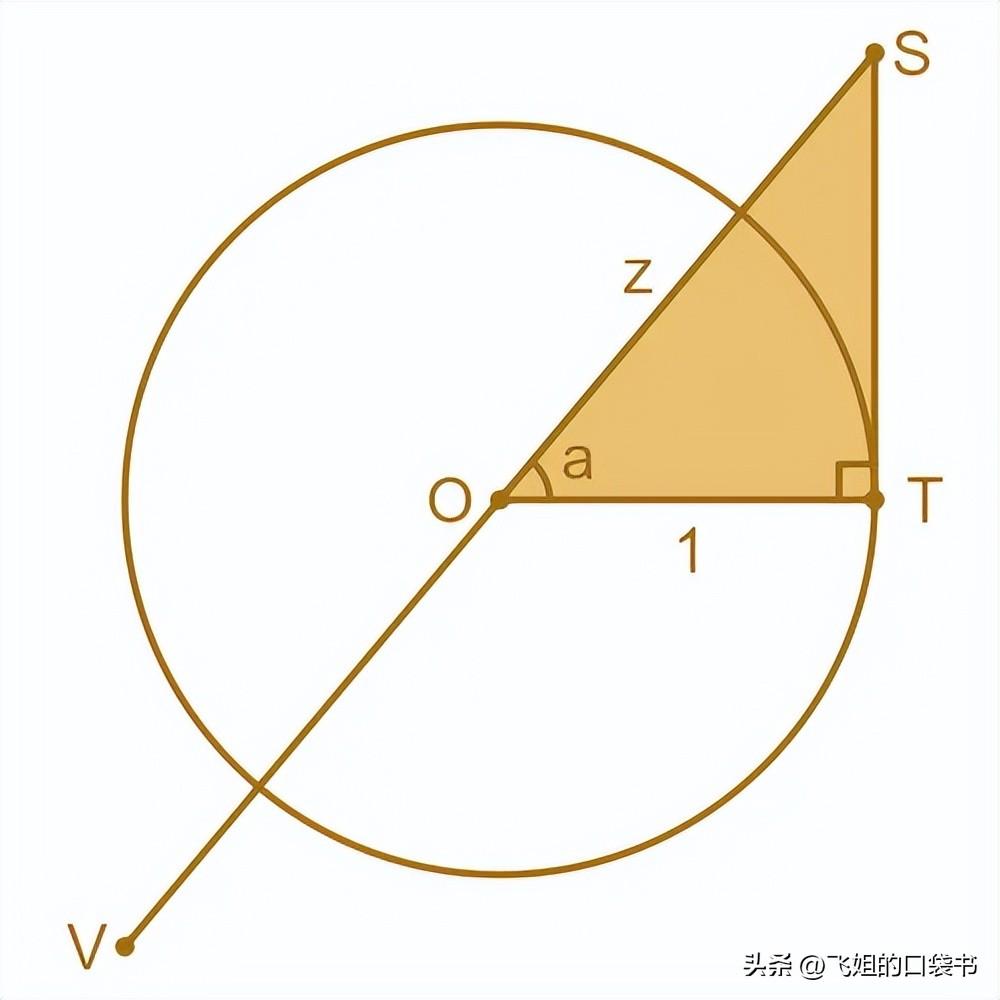
在此图中，斜边SO 的长度为z。邻边OT 的长度为 1，因为它是单位圆的半径。

线SV是圆的割线，因此斜边SO是割线的一部分。

正割函数是余弦函数的倒数，所以定义为：

所以sec a告诉我们长度SO ，它是构成割线SV一部分的三角形边的长度。所以我们称它为正割函数。

二次三角函数 - 余弦、余切、余割

辅助三角函数的名称是通过将前缀co添加到其中一个主要函数的名称而形成的。这表明该函数是基于互补角的。

在直角三角形中，两个锐角a和b称为余角：

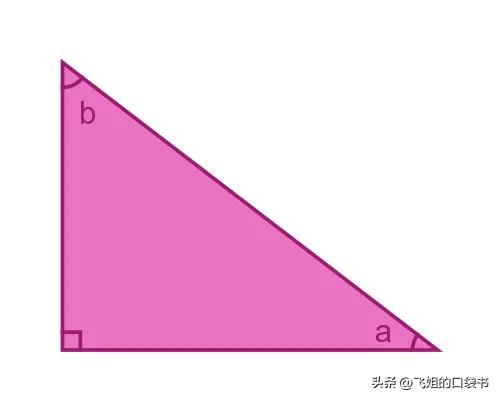
角a和b总和为 90 度。

在三角函数的情况下，主要函数基于圆心的角度（我们一直称之为a）。辅助功能基于互补角b。

余弦函数

这是我们之前用来说明正弦函数的图表，但这次也显示了余角b ：

我们之前已经看过正弦函数的方程式：

需要明确的是， sin a的值告诉我们角度a的长度PQ（即x ） 。cos b的值也告诉我们x的值，但是根据角度b。

当然，边PQ与角a相对，但它与角b相邻，因此替换边名称可以得到余弦的常用公式：

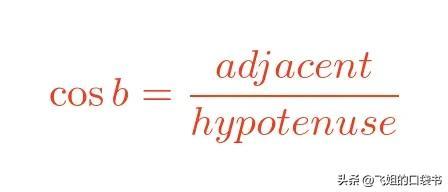
余切和余割函数

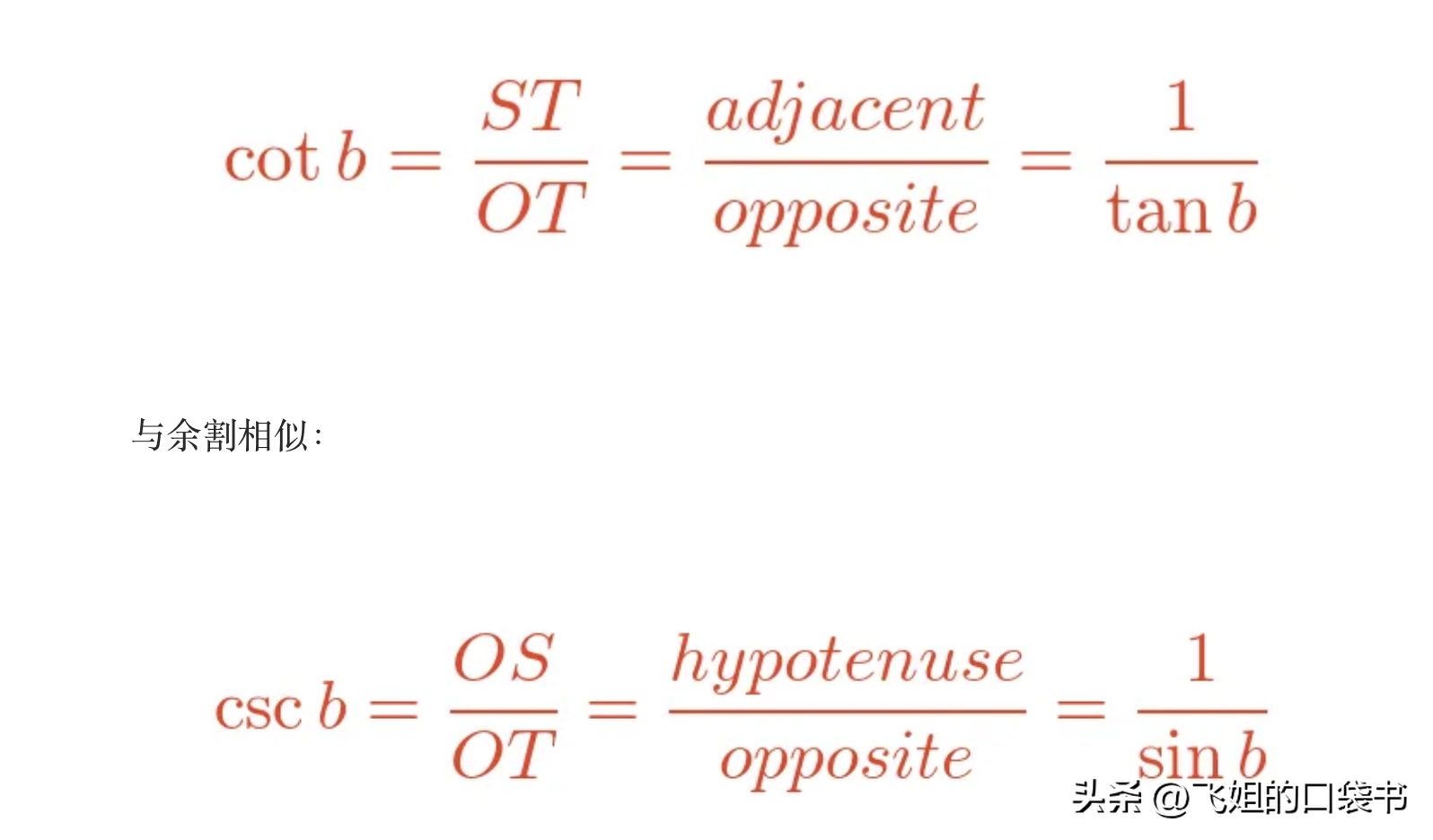
余切函数可以类似的方式找到。我们不会详细讨论它，但是角cot b的公式使用与tan a相同的边，但切换相反和相邻：

反三角函数

反三角函数允许我们从两侧找到角度，例如，如果：

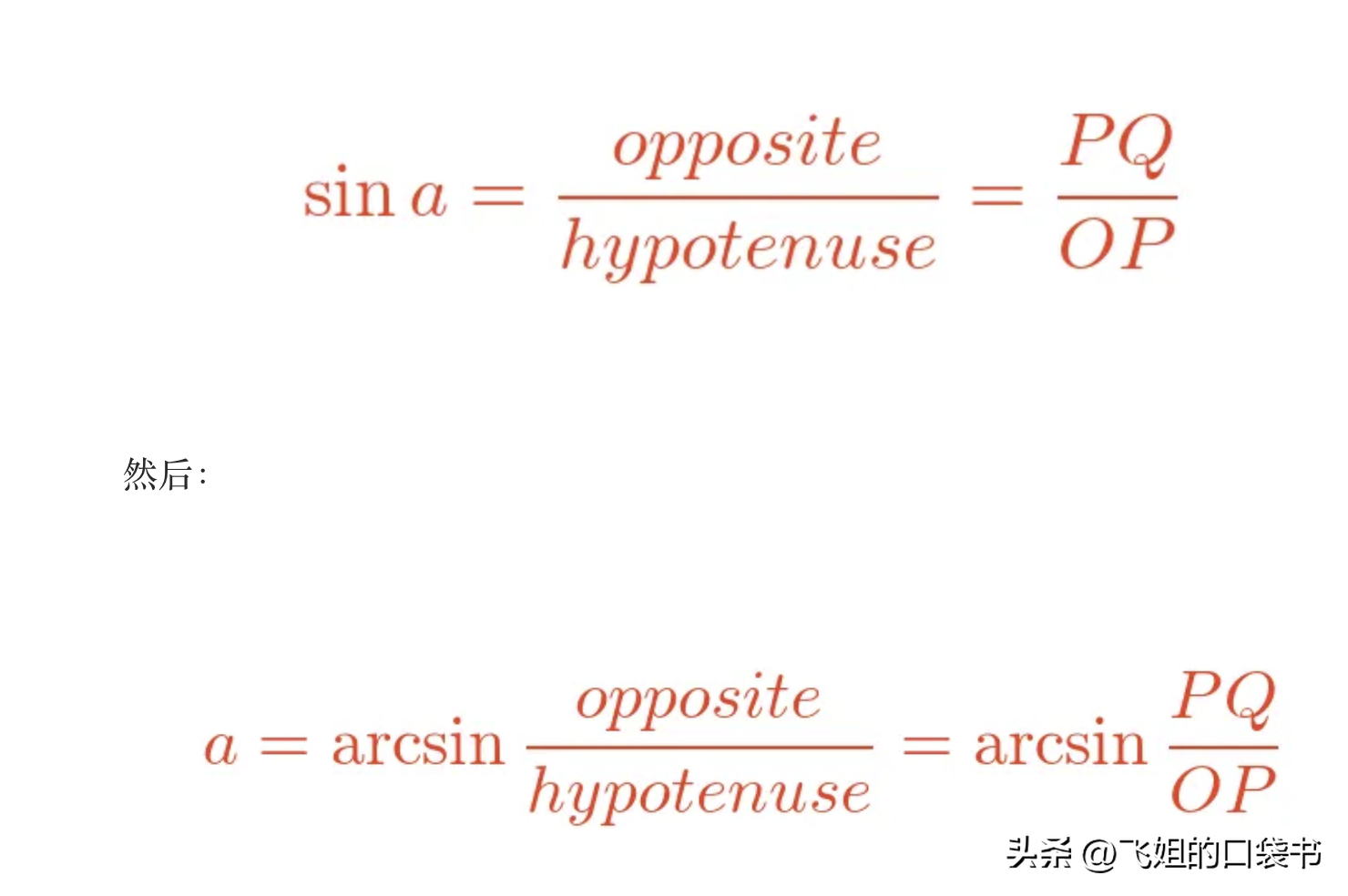
此反正弦函数有时称为反正弦的反正弦。同样，反正切可以称为arctangent或arctan等。

为什么是这样？好吧，如果我们在单位圆的中心以弧度为单位测量一个角度，那么它创建的弧的长度等于该角度。这是arcsin的说明：

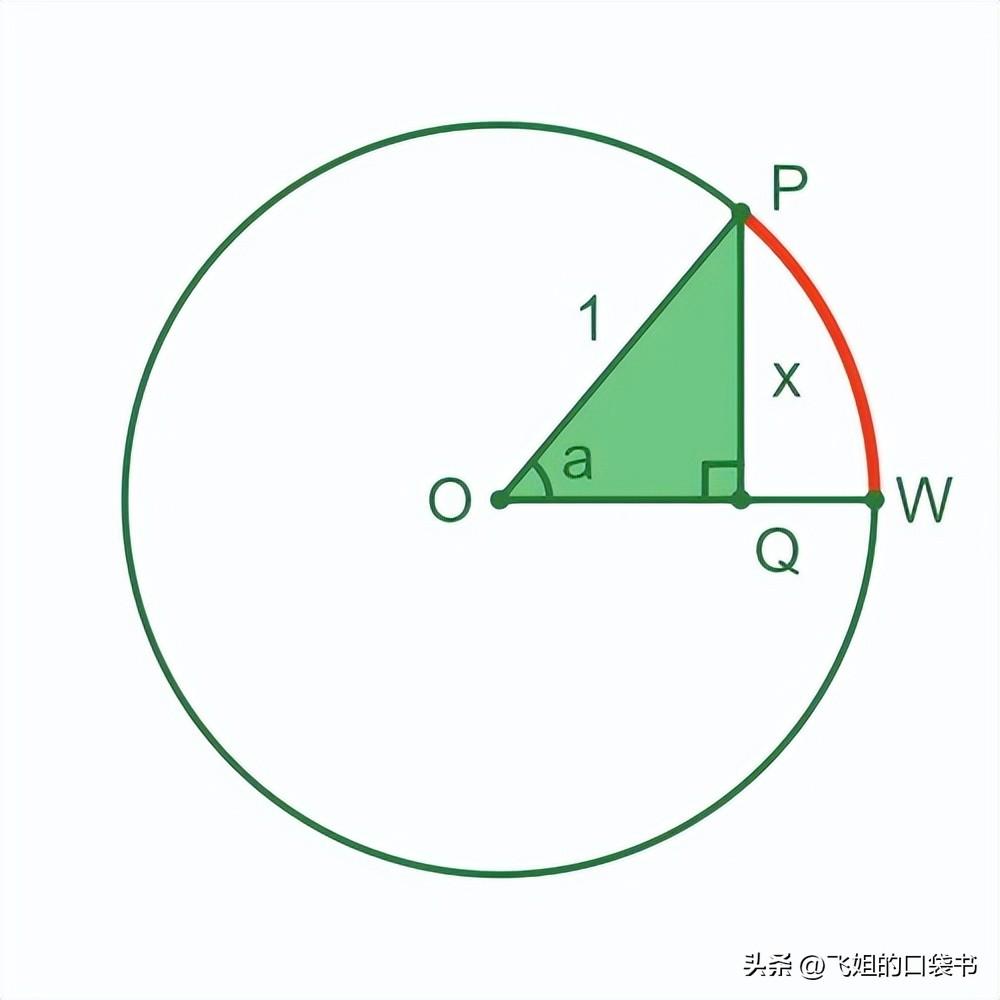
x的反正弦等于圆弧PW的长度。当然，它也等于角度a 。