数学中的曲率,主要是研究曲线的弯曲程度,我们今天一起来看一下。
概念:数学上表明曲线在某一点的弯曲程度的数值。曲率越大,表示曲线的弯曲程度越大。
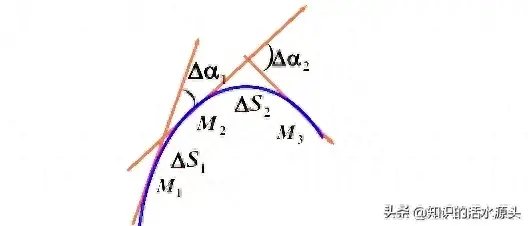
通过上述图片,大家可以看出,弧段弯曲程度越大转角越大,此时曲率就会越大,反之,曲线弯曲程度越小,曲率就会越小。
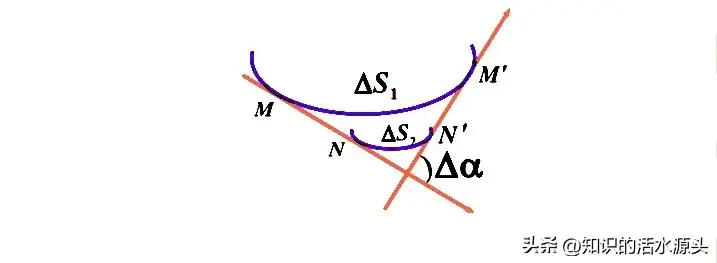
其次就是,不一样长的两条曲线,如果转角相同,弧段越短,弯曲程度越大。此时也可以得到曲率越大。
接下来我们再来看一下有关的曲率计算公式:
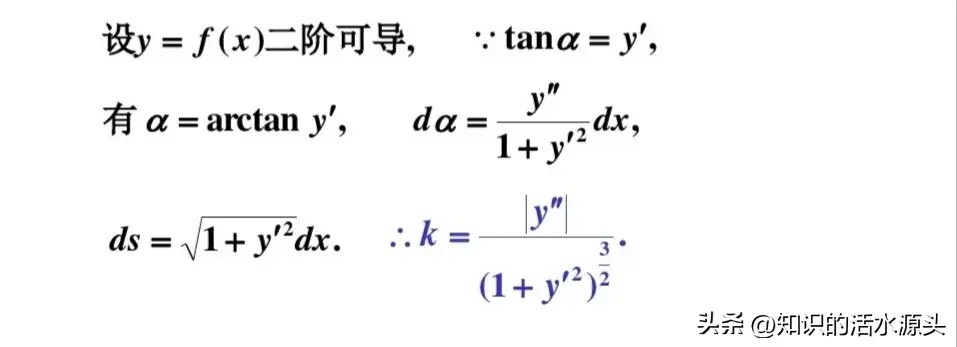
注意:曲线必须可导,存在一阶导,二阶导,此时才存在以上公式。

其次就是参数形式的曲线,如果可导,也可以得到曲率的计算公式,以上公式是根据参数求导法则进行推导的。
我们来看一个例题,以便更好理解曲率概念。
求解抛物线y=ax²+bx+c上哪一点的曲率最大?
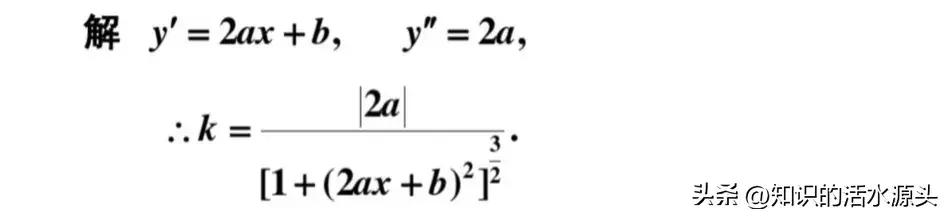
根据题意,我们先求出一阶导和二阶导,然后再根据公式代入。

根据K的表达式我们可以看出,其实在顶点处的曲率是最大的。
接下来,我们再来看一下曲率圆和曲率半径的表达:
定义:设曲线y=f(x)在点M处的曲率K(K≠0),在曲线上的点M处的法线上取一点D,其中D在曲线凹的一边,如果有以下情况:
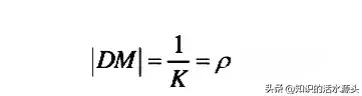
其中以D为圆心,ρ为半径作圆
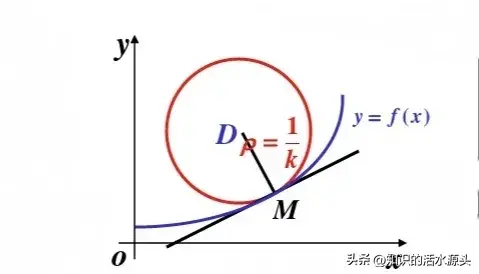
上述图形中,这个圆称为曲线f(x)在点M处的曲率圆。圆心D称为曲线在点M处的曲率中心。ρ称为曲线在点M处的曲率半径。
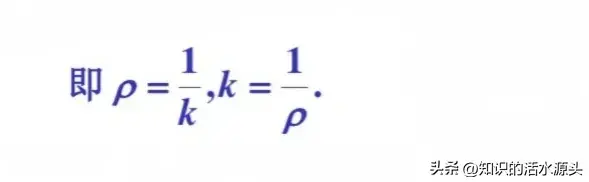
通过上述的学习,我们来做一个题,以便更好的理解知识点:
例题讲解:
求解4x²+y²=4在(0,2)点处的曲率及曲率半径。
解:根据题意,方程两边先对x求导可得以下条件
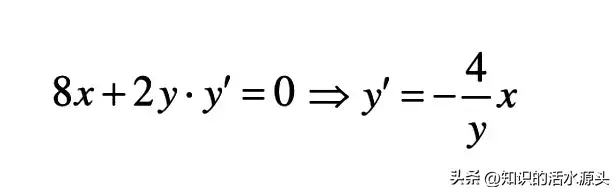
上面式子中,再对x求导可得:
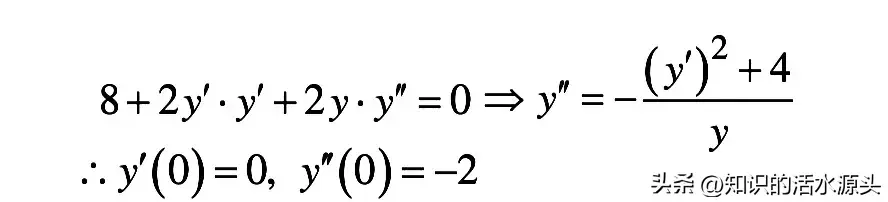
求出一阶导和二阶导过后,再将x=0代入一阶和二阶导数。进而即可求出K在点(0,2)处的具体曲率值以及曲率半径值。
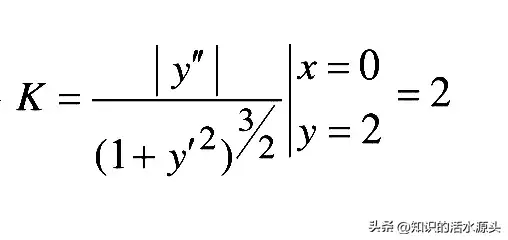
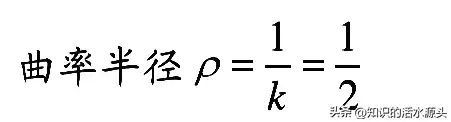
通过学习,大家可以下去做一做以下练习题,以便更好理解:

















