《集合》教学设计
教学目标:
1.让学生经历维恩图的产生过程,能借助直观图,利用集合的思想方法解决简单的实际问题。
2.培养学生善于观察,善于思考的学习习惯。使学生感受到数学在现实生活中的广泛应用,尝试
用数学的方法来解决实际生活中的问题,体验解决问题的策略的多样性。
3.培养学生合作学习的意识和学习的兴趣。
教学重点:
借助直观图,利用集合的思想解决简单的实际问题。
教学难点:
理解维恩图中的各部分,并用规范的语言表达含义。
教具、学具准备:
多媒体课件,课堂练习作业纸。
教学过程:
一、创设情景,引出新知
1.情景引入,出示信息
师:老师在课前了解到我们班有很多写作高手和计算高手,今天我给这些孩子带来了奖状,你们
知道老师准备了多少张奖状吗?瞧!有5张是写作超人和6张计算能手。课件演示信息。
2.提出问题,激发“冲突”
师:你们知道获奖的共有多少人吗?一定是11人吗?有没有其他可能?
二、 自主探究,学习新知
1.独立思考表达方式,经历知识形成过程。
师:瞧这就是获奖名单,我们一起来研究一下,是不是11人呢?
生:是。
生:不是。
师:你有什么好想法吗?现在我们就小组活动,在作业纸上把你的好想法记录下来吧!课件出示
活动要求。
学生独立思考,并尝试解决。
2.汇报交流,初步感知集合概念。
(1)小组交流,互相介绍自己的作品。
(2)选择有代表性的方案全班交流。
在小组时汇报时引出重叠,并板书重叠。
3.介绍维恩图,运用数形结合解决问题。
(1)介绍用维恩图表示集合。
师:同学们在数学上我们还可以把获得写作超人的学生看作一个整体,叫做一个集合,把获得计
算能手的学生看作一个整体,也是一个集合。(边介绍集合,边课件演示)。
师:这就是我们今天要研究的新知识集合,板书课题:集合。
师:现在老师把获奖名单去掉,只剩下了两个椭圆,(一个是红色的, 一个是蓝色的),它们重叠
了吗?(没有)怎么样能让它们重叠呢?指名上台移一移(重叠的部分变成紫色)。
师:谁知道为什么会变成紫色?
师:是的,这里面还蕴藏了一个美术小知识,当红色和蓝色混在一起就会变成紫色,所以紫色里
面既有红色又有蓝色。引出关联词既……又……,并板书:既……又…….。
再指名学生尝试说一说其他部分的含义。
师:那现在你们能把重新给这些获奖名单找到合适的位置吗?课件出示,指名学生上台拖动名单,
演示过程。
(2)运用数形结合思想,介绍集合的运算。
师:我们研究发现获得写作超人奖状的有5人,获得计算能手奖状的有6人,它们重叠部分既是 写作超人又是计算能手的有2人,获奖的共有是多少人?(课件演示)你们能用列算式的形式来
解决这个问题?
让学生尝试独立解决,再汇报交流,体会解决问题的多种方法。板书算式。
师:我们求的结果,对不对呢?现在请这些获奖的同学上台领奖,来我们一起来验证一下吧!通
过发奖状验证是9人。
(3)小结
师:刚才我们在图中找到了数,用这些数解决了实际问题,这就是数形结合。板书:数形结合。
师:其实利用数形结合的方法可以解决很多的生活中的难题。
(4)介绍维恩图的由来。
课件出示你知道吗?
三、 联系生活,巩固练习。
1.完成第105页“做一做”第一题。
师:现在我们一起来放松一下吧,我们去动物王国看看吧,(课件出示动物图, 一一介绍动物的 名称),你们见过大雁吗?我们一起看一个小视频了解一下它的生活习性吧,(课件播放介绍大雁
的视频,引出它既会飞又会游泳)。
师:现在你们根据它们的生活习性,能把这些动物的序号填在合适的圈里吗?在填之前我们先来
看看每个圈的要求吧,请同学们在作业纸上完成这道题吧,指名学生上台汇报。
2.完成第106页练习二十三第一题。
师:数学来源于生活,生活中还有很多问题,也蕴藏着集合思想。课件出示水果题。
先引导学生分析题意,再指名学生回答发现重叠部分,课件移动水果的位置,并把重叠的一一对
重叠
既…………..又…..
数形结合
应连线。
师:同学们思考一下,在这里的几个算式中哪个是正确的?指名回答,希沃课堂活动设置验证。
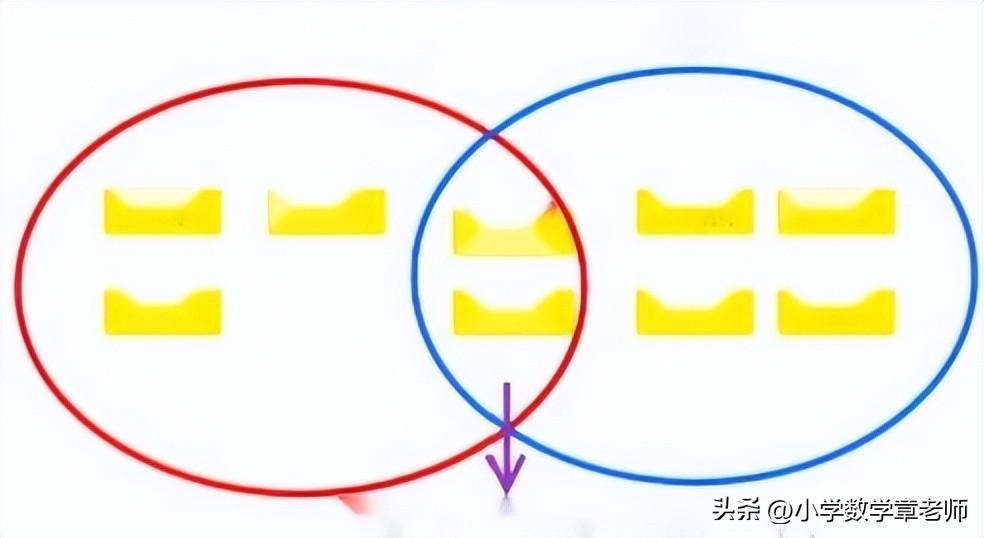
3.拓展延伸,出示木棒题。
师:你们真厉害,刚才的问题轻松就解决了,现在老师要增加难度了,你们有信心解决吗?一起
来看看是什么问题吧!
课件出示木棒题,先读清要求,指名学生上台通过移动木棒,感知解决问题的方法,学生再独立
完成。
四、 知识梳理。
师:这节课我们先经历了解决生活中的问题,通过自主探究,利用数形结合,找到了合适的方法, 了解了简单的集合知识,又运用集合思想去解决实际问题,发现集合思想是无处不在,只要是我
们会灵活运用,就能去解决更多更难的问题。
五、 板书设计:
集合