不知我们是否有这种想法,数学书有时会不好好说话,出现所谓的奇怪“规定”,规定分母不能为0,规定0的阶乘是1,规定负负得正……
其实哪里有那么多规定,所谓的“规定”都是有原因的,只是考虑到不同阶段学生的理解能力,教材才采用了这种粗放式的表述方式。然而对于一个善于思考的人,探寻这些“规定”背后的逻辑,正是我们发现数学奥秘的一个个窍门。
比如,思考为什么分母不能为0(除数不能为0)。要知道除法和乘法互为逆运算,除数为零时,就是要找一个数乘以零等于被除数,当被除数不为零时,这显然是找不到的(任何数乘以零都等于零)。那0/0该等于什么呢?按照与乘法互逆的规则,这结果可以等于任意数(当然这里0/0是纯粹两个0相除,不是“洛必达法则”中两个极限值为零的变量的比,即“不定式”)。但正因为0/0可以等于任意数,当有人问0除以0等于什么时,我们可以乱答一个数,那都是对的,这样是不利于数学研究的规范性的。
为了数学世界的“整洁”,我们就统一做规定0不能为除数。
那是否可以成立一个学派,在这个学派中强行让0/0有意义,比如记0/0=ψ, ψ表示任意一个实数。当然这个学派不要和主流数学界有相关的交流(毕竟道不同不相为谋)。顺便想一下,你认为这个学派下函数y=0/x的定义域会是什么?还有函数y=x⁰呢?
就如现在也有一些学派认为0不是自然数。要知道,国内和国外对于0是不是自然数历来有两种规定:一种规定0是自然数,这是大多数国家,另一种规定0不是自然数,如日本。建国以来,我国中小学教材一直规定自然数集合不包括0。现在,国外的数学界,大部分都是规定0是自然数,为了国际交流的方便,1994年11月国家技术监督局发布的《中华人民共和国国家标准,物理科学和技术中使用的数学符号》中规定,自然数集包括0。
数学上的一些“规定”本质上是运算规则适配的产物。
为什么0的阶乘是1?初始的设定就是为了让阶乘的计算规律适配到0上。

将阶乘运算规则进一步适配到实数域和复数域还产生了神奇的伽马函数(Gamma Function),这也是欧拉大神的杰作:
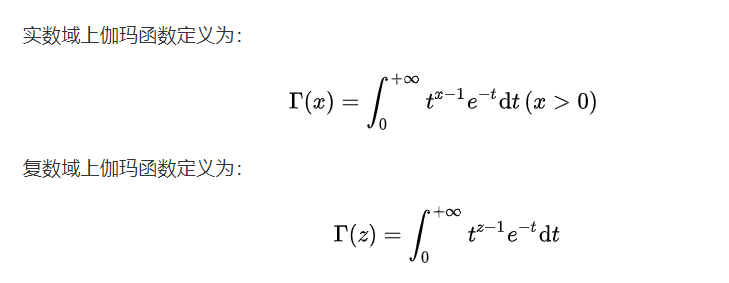

不禁向数学先驱致敬。不过,这其中的原理十分复杂,以后专门写文章来叙述。
而且乘法中的“负负得正”本质上也是运算规则适配的结果:
将乘法分配律应用于负数便会产生“负数乘以负数等于正数”。
如下,若将乘加分配律用于下式:
0 =(-1)× (1 + (-1))= (-1)×1 + (-1)× (-1)
就必须有:
(-1)×(-1)= 1
对于“负负得正”,前面也有文章论述过——为什么“负负得正”?
在一个看似平淡的地方若有所思考,这便能挖掘出数学的乐趣。因为数学带给我们的不能仅仅是会做数学题。
那你可能会说为什么数学书不把“规定”背后的原因说清楚,而要强行用规定来描述。
要知道数学的通俗性和严谨性往往是很难兼具的,一个小小的规定,也可能水很深。例如在纯代数背景下,若不引入极限语言,你甚至很难说清楚为什么y=x²的值域是 [0,+∞)。
你可能会说,如此显然的事情我为什么要去说清楚或证明呢?凭直觉就能搞明白。不应该将思考浪费在这种小问题上?
当年毕达哥拉斯学派的人也是这样想的,认为两个有理数可以靠的任意近,所以数轴上除了有理数就没有其他的数了。
结果呢?大家都知道,被啪啪打脸。
这件事以后,数学家害怕了,觉得直觉可能靠不住,可能指不定哪天一个大家“看上去”很对的命题直接被人揪出一个反例,把前面所有数学家都羞辱一遍。于是数学家开始对数学命题给出严格的逻辑证明。
在不需要思考的地方思考,这是十分难得的。
要知道按照人的直觉经验,地球是平的,就像这样:

要不怎么会有“天圆地方”的观点。然而早在古希腊,亚里士多德便通过思考得出了地球是球形的论述。在他公元前350年写的《论天》一书中,提出了几个地球为球形的论据:
1、远航的船不是一点点变小而最终消失,而是桅杆随着船身慢慢沉大海,并且船从远处驶来,在海天交接处总是先看到桅杆再看到船。
2、在同一时间,同样的木杆在地球的不同地方影子的长度不同。
3、人们沿着南北方向运行时,所看到的星空不完全相同,有些星座会消失,有些新的星座会出现,如在埃及有一些星星在600英里外的塞浦路斯看不到。
4、月食发生的过程中地球在月亮上的影子是弧形的。

稍晚一点的埃拉托色尼甚至在地球是球形的基础上第一次测量了地球的周长(测量所在地的子午线长,即经线圈周长),要知道这可是发生在2000多年前。
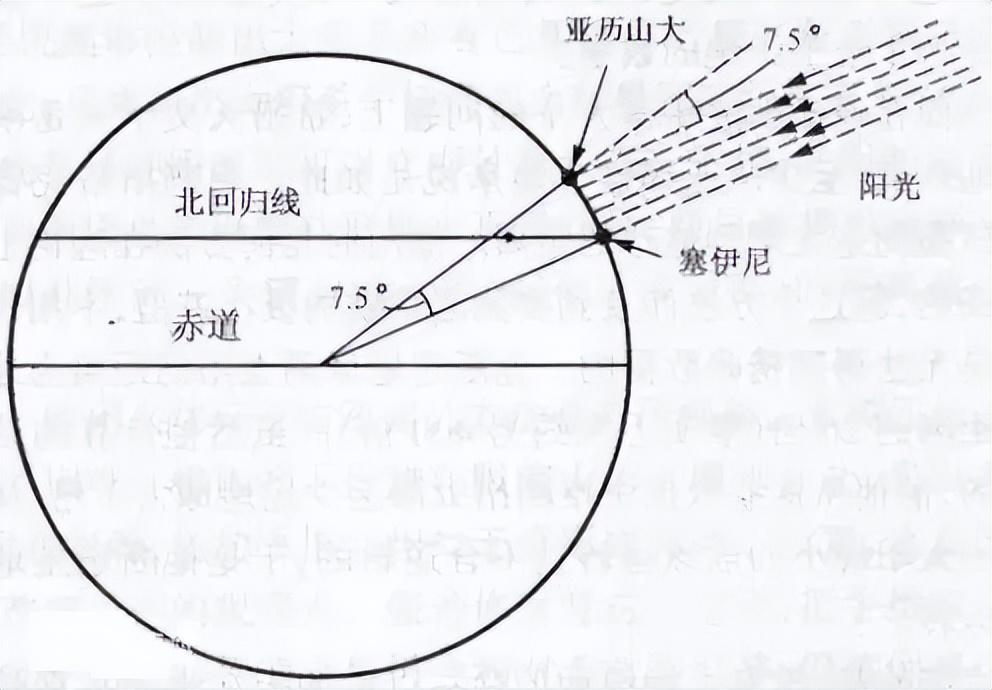
要不怎么说数理逻辑和形式逻辑起源于古希腊呢,中世纪欧洲文艺复兴大量涌现追溯古希腊的思潮,这促成了科学从哲学中分离,并在牛顿时代数学辉煌的照耀下最终形成了现代科学(科学是一套完整的实验体系和方法论)。
是思考赋予了人类的伟大。
依靠睿智的“大脑”,使得从未离开过太阳系的人类(人造探测器最远也没飞出太阳系,而人的足迹最远只到过月球),居然有能力探寻宇宙的秘密:
从光谱到宇宙:
















