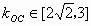
结论1、过抛物线的焦点F的直线l交抛物线于A、B两点,设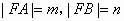 ,O为原点,则有:
,O为原点,则有:
(1)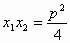 ;(2)
;(2)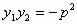 ;(3)
;(3)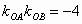 ;(4)
;(4)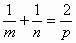 。
。
结论2、直线l交抛物线于A(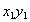 )、B(
)、B( )两点,O为原点。若OA⊥OB,则直线l经过定点(2p,0),
)两点,O为原点。若OA⊥OB,则直线l经过定点(2p,0),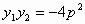 ,反之亦然。
,反之亦然。
例1、过抛物线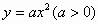 的焦点F,作一直线交抛物线于P、Q两点,若线段PF、FQ的长分别是p、q,则
的焦点F,作一直线交抛物线于P、Q两点,若线段PF、FQ的长分别是p、q,则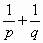 等于
等于
A. 2a
B.
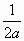
C. 4a
D.
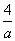
解:将抛物线方程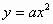 ,化为
,化为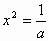 y,从而由结论1中的(4)知,本题正确答案应选C。
y,从而由结论1中的(4)知,本题正确答案应选C。
例2、设抛物线E为,AB和CD为过焦点F的弦。求证:(1)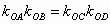 ;(2)以AB与CD为直径的两圆的公共弦必过原点。
;(2)以AB与CD为直径的两圆的公共弦必过原点。
证明:(1)由结论1中的(3)知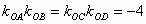 。
。
(2)设A、B、C(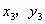 )、D(
)、D(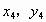 ),
),
则以AB为直径的圆的方程为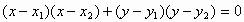 ,
,
以CD为直径的圆的方程为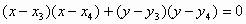
两式相减并整理得公共弦方程:
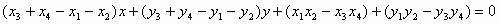
由结论1中的(1)(2)知:
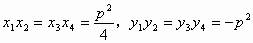
则公共弦方程中常数项为0,故公共弦必过原点。
例3、设抛物线的焦点为F,经过点F的直线交抛物线于A、B两点,点C在抛物线的准线上,且BC//x轴。证明:直线AC经过原点O。
证明:设A、B,由结论1中的(2)知
∵BC//x轴,且点C在抛物线的准线上,
∴点C的坐标为
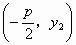
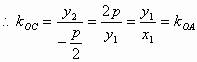
则直线AC经过原点O。
例4、已知抛物线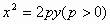 ,动直线l交抛物线于两点A、B,且,O为原点,O在l上的射影为H。
,动直线l交抛物线于两点A、B,且,O为原点,O在l上的射影为H。
(1)求点H的轨迹方程。
(2)设过A、B、O三点的圆的圆心为C,直线l的倾斜角的范围为
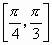
,求直线OC的斜率的取值范围。
解:(1)因为,
由结论2知:直线l经过定点M(0,2p)。
由OH⊥l,得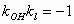
设H(x,y),则
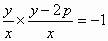
∴所求点H的轨迹方程为: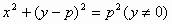
(2)因为,由结论2知:OA⊥OB,则圆心C为AB的中点,
故可设直线l方程为: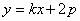 ,
,
代入抛物线方程消去y得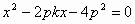
由中点坐标公式,求得C(pk,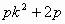 ),
),
则
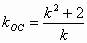
又由题设知: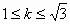 ,从而求得
,从而求得