第1单元 小数乘法

第1课时 小数乘整数
课题 | 小数乘整数 | 新授课 |
教学目标 | 1.使学生理解小数乘整数的算理,掌握小数乘整数的一般方法,会比较熟练地进行笔算。 2.使学生经历将小数乘整数转化为整数乘整数的过程,自主探索小数乘整数计算方法的过程,渗透转化的数学思想,培养简单的逻辑推理能力。 3.使学生体会小数乘法在实际生活中的应用,感受数学源于生活,生活需要数学,形成积极的学习态度。 | |
教学重点 | 掌握小数乘整数的一般计算方法 | |
教学难点 | 理解小数乘整数的算理 | |
教学准备 | 课件 | |
课时安排 | 1课时 | |
教学过程 | 导案 | |
一.情境创设,揭示课题 | (一)课件呈现,寻找信息 1.课件呈现“放风筝”的情境以及各种不同形状的风筝。 2.课件呈现“买风筝”的情境(例1的主题图),画面上醒目地显示四种形状各异、价格不同的风筝。 3.设问:从图中你能看出哪些数学信息? (二)提出问题,揭示课题 1.这节课我们就一起先来解决“买3个蝴蝶风筝多少钱”的问题,你能列出算式吗?(教师板书或PPT课件呈现:3.5×3=) 2.追问:这个算式和我们以前学过的算式有什么不同呢? 3.引导:今天我们就来学习小数乘整数。(板书课题:小数乘整数) | |
二.自主探索,兴趣维持 | (一)感知算理 1.算一算:3.5×3,可以怎样计算? 给足时间,让每一位学生根据自己的知识和经验独立计算出买3个蝴蝶风筝所需的钱数。教师巡视,注意发现学生中的不同计算思路。 2.说一说:你是怎样计算的? 学生的计算思路可能有:用加法进行计算;改写为复名数进行计算;化“元”为“角”进行计算等。 (二)重点分析、研讨化“元”为“角”算法的算理 1.组织全班学生对上述多种不同解法逐一进行分析、评价和充分肯定。 2.引导学生着重分析化“元”为“角”的计算方法。 (1)师:上述几种算法中,你认为哪种算法比较简单?这种算法中的关键是什么? (2)学生分析、对比、讨论后,引导学生用简洁的话总结、概括:先把3.5元转化为35角,再计算35角×3,最后将结果105角转化成10.5元。 (3)教师边小结边适时板书(或PPT课件动态呈现)如下竖式计算过程: 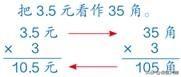 (4)小结:刚才我们在解决“买3个蝴蝶风筝多少钱”的问题时,想到了各种不同的计算方法。我们发现以“元”作单位的小数乘整数,可以转化成以“角”(或“分”)作单位的整数乘整数来进行计算。 (三)运用转化,探究算法 动态呈现小数乘整数的过程 1.出示算式0.72×5=?,提问:“0.72不是钱数,怎样计算?” 2.让学生独立思考,再引导学生提出:“能不能转化成整数来计算?” 3.学生尝试列竖式计算。(教师巡视,了解学生的计算方法。) 4.小组交流计算方法。 5.学生全班集体交流转化过程和计算方法,教师适时板演(或PP课件演示)乘法竖式计算过程,帮助学生理解算理算法。 (教师重点引导学生理解三点:怎样把因数0.72转化成整数?乘得的积应如何处理?积末尾的“0”如何处理?从而使学生更好地理解算理。) 由于因数0.72化成整数72必须“×100”,所以要使积不变,积360应“÷100”。 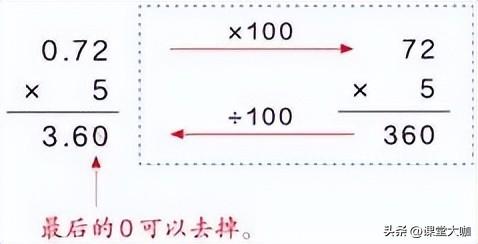 将乘得的积化成最简小数 请学生观察乘得的积“3.60”,提问:3.60是最简小数吗?(不是!)提醒学生,乘得的积如果不是最简小数,可以根据小数的基本性质将积中小数末尾的0去掉。 | |
三.寓教于乐,兴趣体验 | 互动环节: 学生先独立完成教材P3的“做一做”,做完后和同桌相互检查,相互指正,最后老师给出正确答案。 | |
四.课堂总结 | 这节课我们学到了什么?你是怎么学会的? | |
教学板书 | 小数乘整数 例1:3.5×3=10.5(元) 例2:0.72×5=3.6 竖式计算: 竖式计算: ×100 3.5元 3 5 角 0.72 72 × 3 × 3 - 5 × 5 ÷100 10.5 1 0 5 3.60 360 | |
教学反思 | 由于小数乘法和整数乘法之间有着密切的练习,因此要仅仅抓住这种联系,引导学生理解算理,将未知转化为已知,将抽象转化为具体。本课时难点不是小数乘整数的计算方法,而是对算理的理解和感悟,因此,在教学过程中应给学生充分思考的机会,重点将时间放在算理上,只有充分理解了算理,才能更好地进行计算。 | |
教师点评和总结: | ||
















