题目如下:
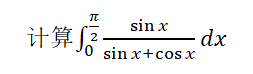
注:该道题来源于我们的课本和一些相关的高数辅导书,同时也是郑州大学2022年数学分析考研真题中的定积分计算题。
解法1如下:
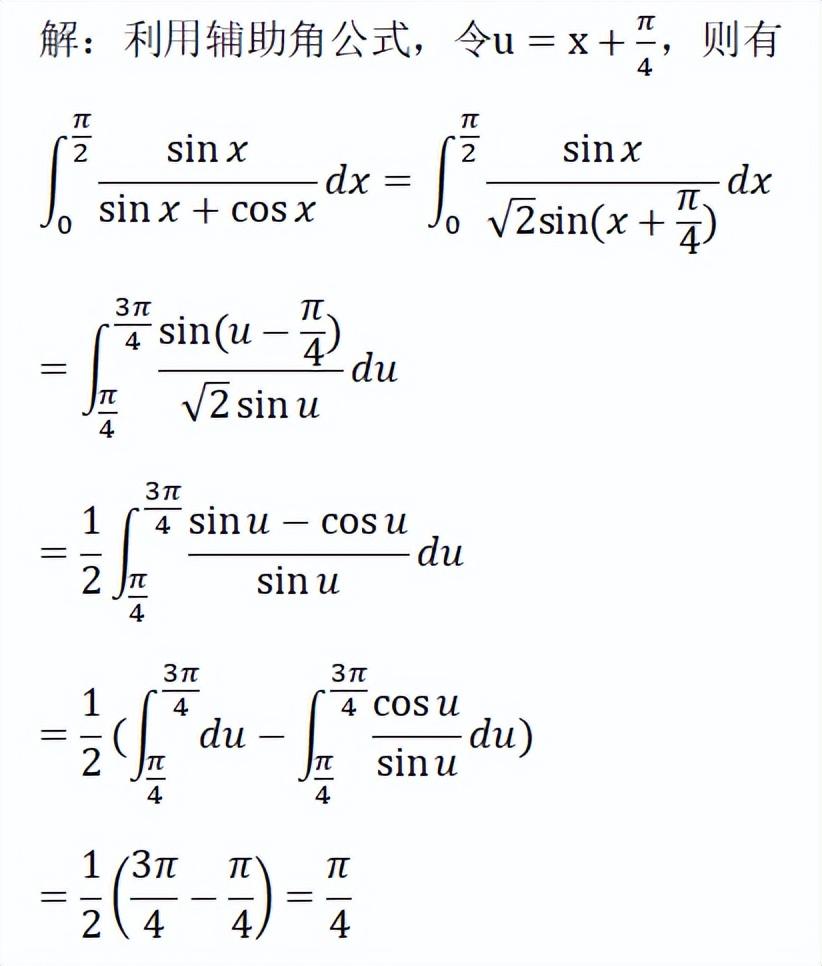
这种做法是最常规的,也是最简单的。解题思路:对sinx+cosx使用辅助角公式,可将分母化为(根号2)*sin(x+π/4),然后再采用换元法令u=x+π/4进行计算,就可以得到积分的结果。
解法2如下:
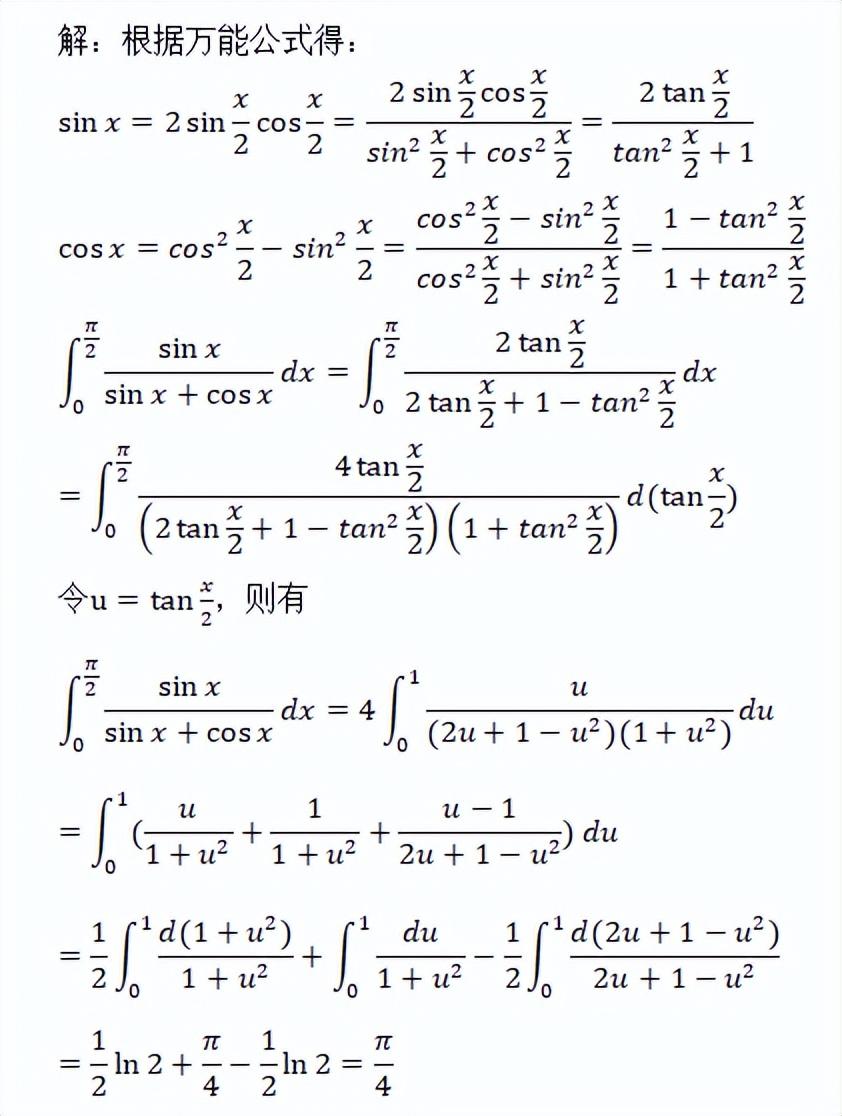
这种做法是最繁琐的,计算量也是最大的。该方法属于高等数学中有理函数积分的一种计算方法。解题步骤:先采用万能公式将被积分函数中的正、余弦函数化为只含有正切函数的式子;然后再采用换元法将正切函数换掉后,得到有理函数;最后对有理函数进行多项式分解,再逐项积分就可以得到计算结果。
解法3如下:
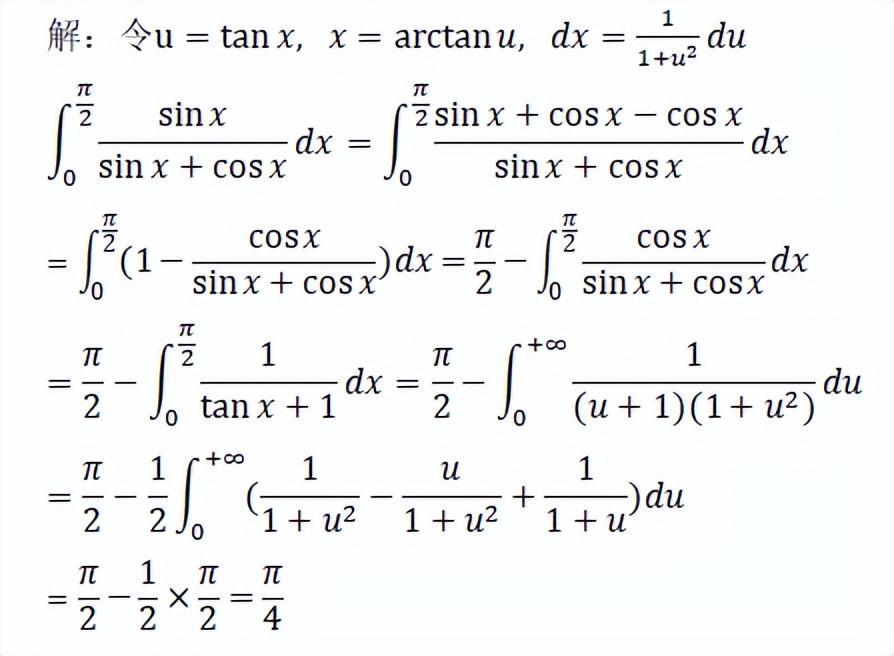
这种做法具有一定的技巧性,需要对被积分函数的分子进行加减一个cosx,然后再对cos x/(sin x+cos x)的分子分母同除以cos x得到1/(tan x+1),再进行换元后得到一个有理函数,最后通过有理函数积分的计算方法得到积分结果。
解法4如下:
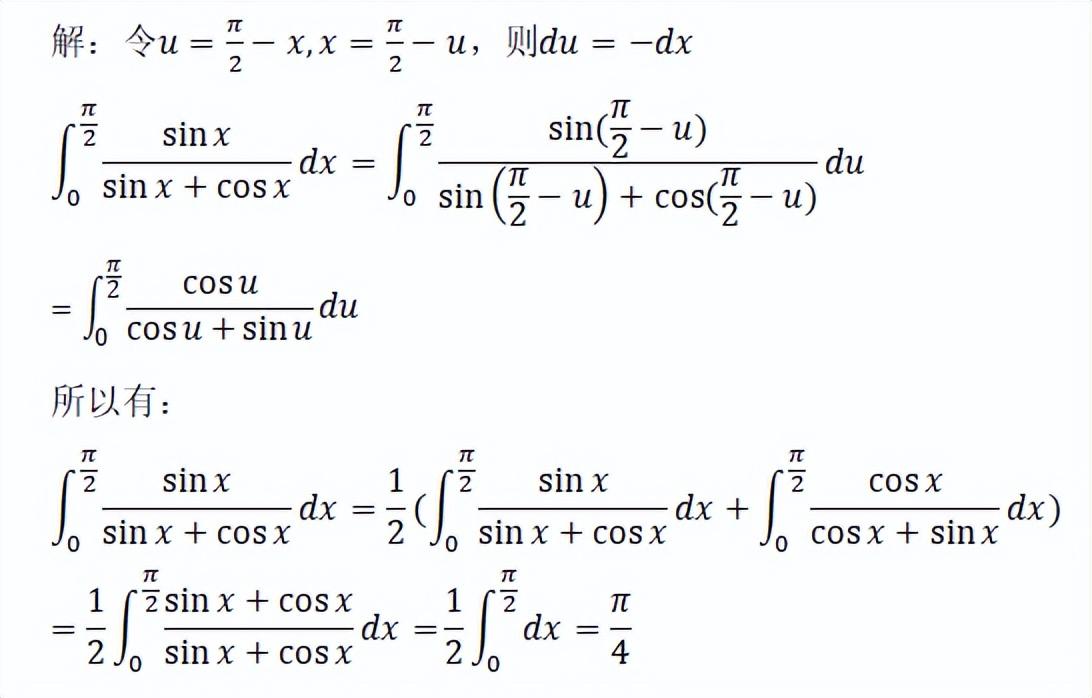
这种解法利用了积分区间再现,即通过换元法令u=π/2-x后,积分区间与原来保持一致,而被积分函数变成了cos x/(cos x+sin x),最后就可以得到题目的计算结果。
解法5如下:
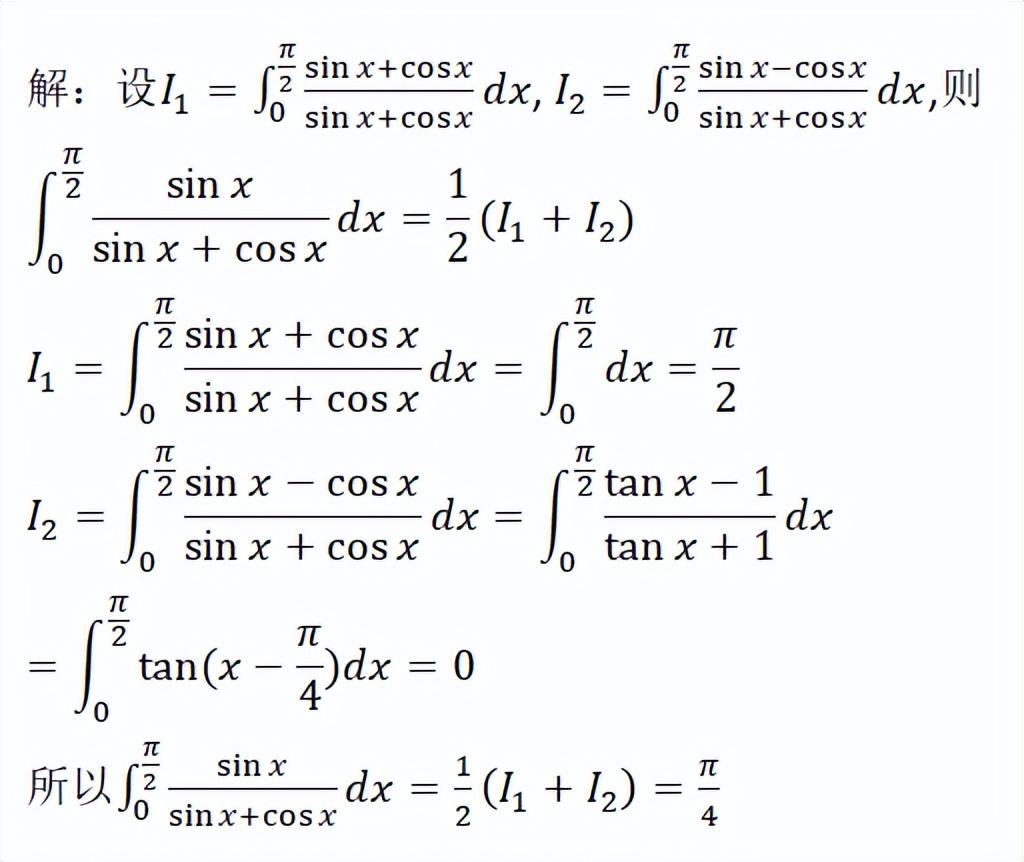
这种解法技巧性比较强,需要构造两个积分,使得要求解的积分能通过这两个构造积分进行表示,而且这两个构造积分一定是易求解的。
















