初中七年级数学---垂线---教案

课 题

垂线

第 周

第 课时

教

学

目

标

1．理解垂线的定义；

2．掌握垂线的性质并会应用；

3．会过一点画已知直线的垂线．

教学重难点

重点：垂线的概念和性质．

难点：理解垂线的性质，过一点画已知线段或射线的垂线．

教学准备

两块三角板

课时安排

两课时

教 学 过 程

一、创设情景 明确目标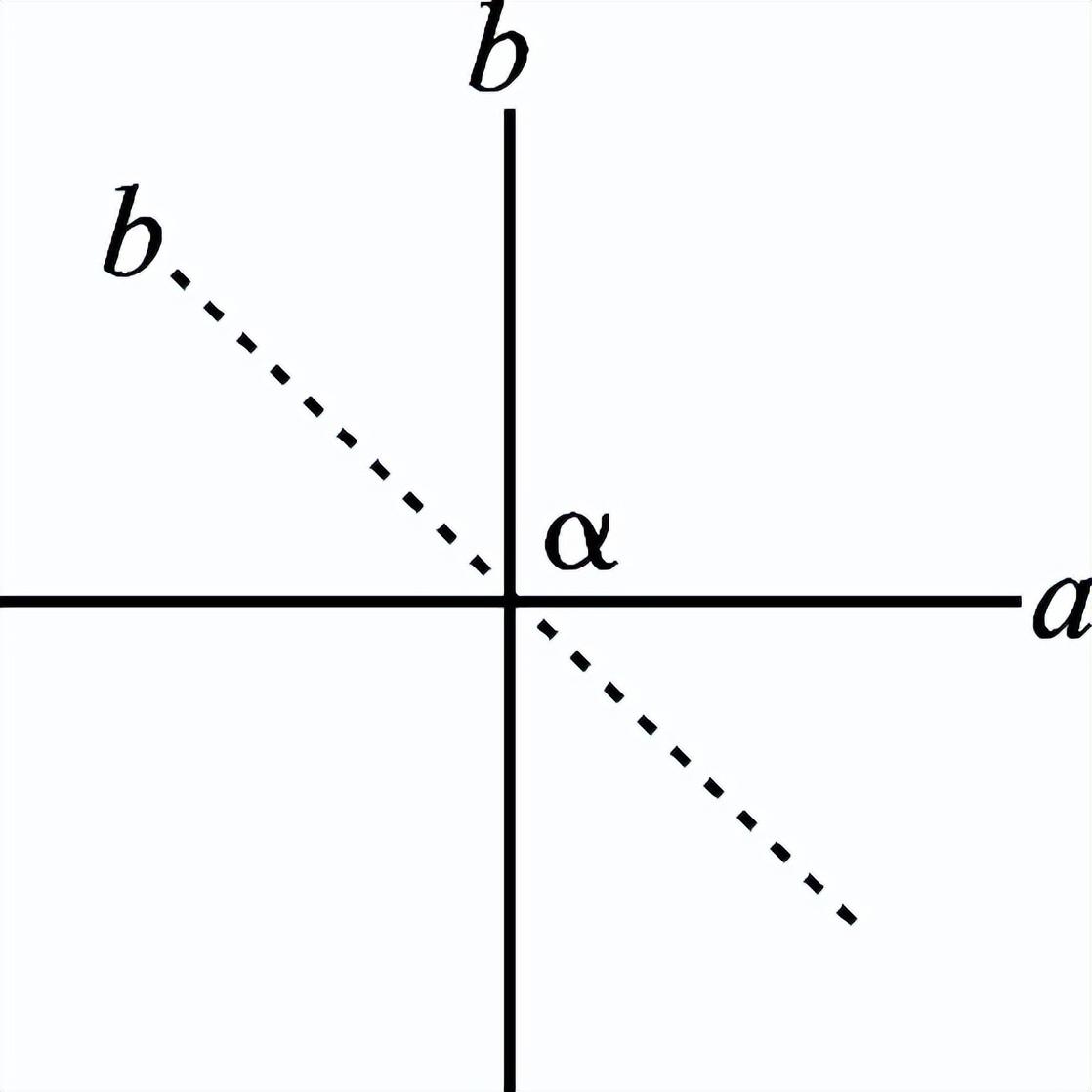

上节课我们已经探讨了两条直线相交共形成四个角，在相交线模型中，固定木条a，转动木条b，当b的位置发生变化时，a、b所形成的角α也会发生变化，当b旋转到什么位置时两直线互相垂直？

二、自主学习 指向目标

自学教材第3至5页，请完成学生用书部分．

1．当两条直线相交所成的四个角中，有一个角是 直角 时，就说这两条直线互相垂直，其中一条直线叫做另一条直线的 垂线 ，它们的交点叫做 垂足 ．

2．过一点有且只有 一条 直线与已知直线垂直．

3．如果直线AB⊥CD于O，那么∠AOC＝ 90° ．

三、合作探究 达成目标

一 垂线的概念

活动1：

阅读教材第3页至第4页，思考下列问题：

(1)两条相交直线在什么情况下是垂直的？什么叫垂线？什么叫垂足？

(2)垂线是一条直线还是线段？

(3)请举出生活中垂直的例子．

(4)在数学中我们用什么符号表示两条直线互相垂直？

展示点评：

请用数学符号表示右图中垂直的推理过程．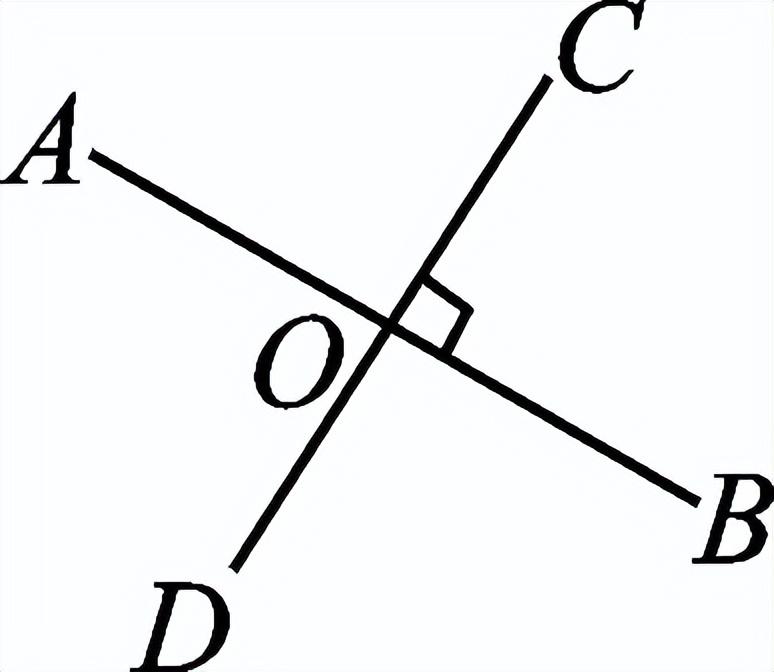

∵∠AOD＝90°

∴______⊥______(　　　　　　　　　　　)

或者是：∵AB⊥CD

∴∠AOD＝______°(　　　　　　　)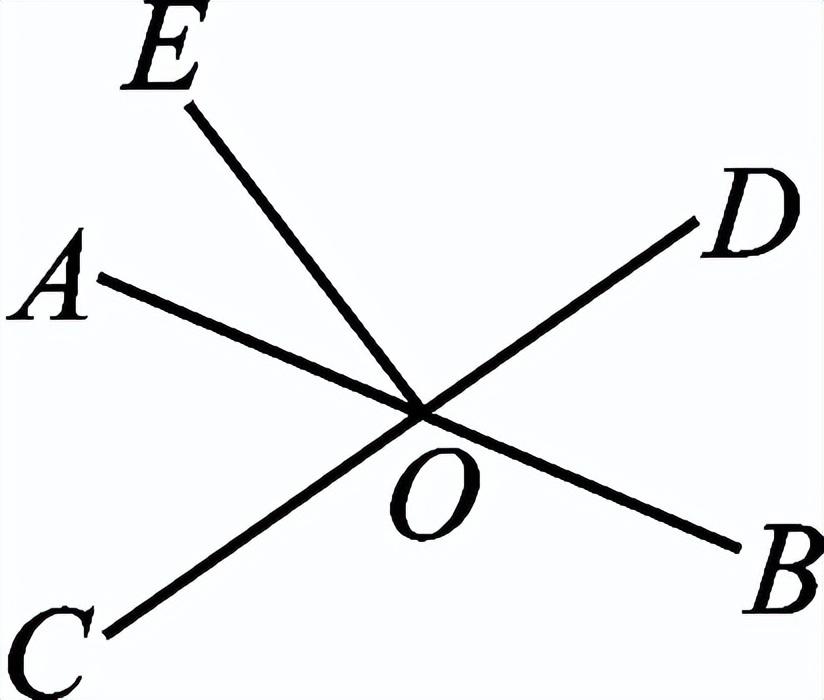

例 如图，直线AB、CD相交于点O，OE⊥CD于O，∠AOE：∠COE＝1∶3，求∠BOD的度数．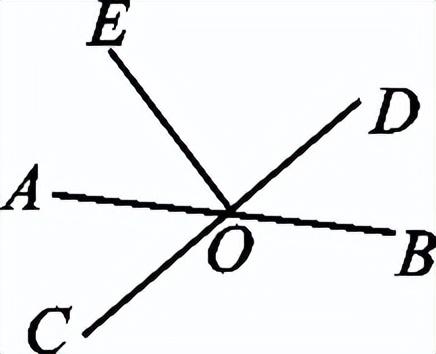

变式：如图，直线AB、CD相交于点O，若AO平分∠COE，且∠BOD＝45°，判断OE与CD的位置关系，并说明理由．

小组讨论：两条直线垂直与相交是什么关系？

反思小结：两条直线相交所得四个角中有一个角是90°时，这两条直线垂直，反之也成立．垂线的定义有判定和性质的双重作用，即知直角得线垂直，知线垂直得直角．垂直是相交的一种特殊情况．

针对训练

1．判断以下两条直线是否垂直：

(1)两条直线相交所成的四个角中有一个是直角．( 垂直 )

(2)两条直线相交所成的四个角相等．( 垂直 )

(3)两条直线相交，有一组邻补角相等．( 垂直 )

(4)两条直线相交，对顶角互补．( 垂直 )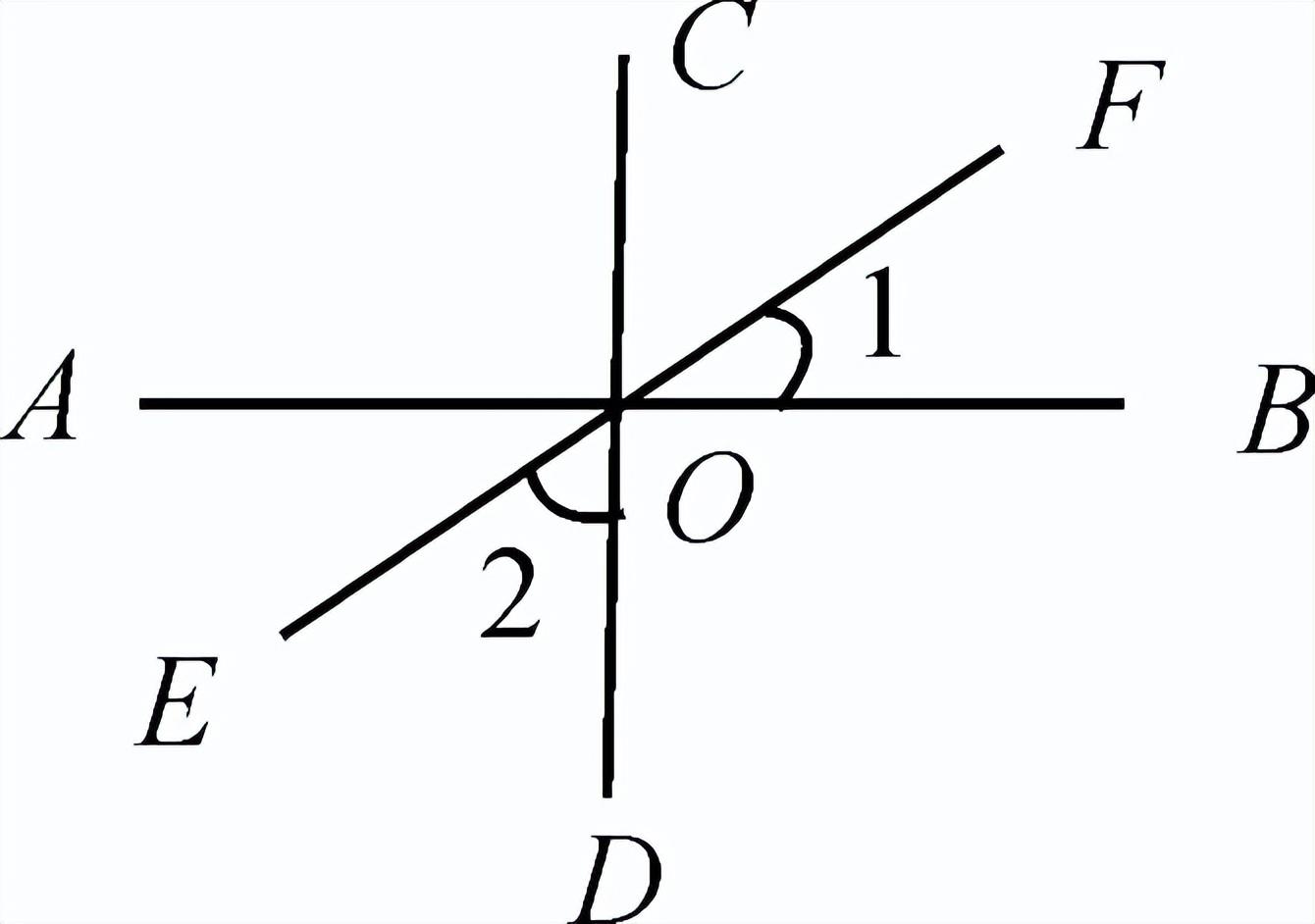

2．如图，已知AB⊥CD，垂足为O，图中∠1与∠2的关系是( B )

A．∠1＋∠2＝180° B．∠1＋∠2＝90°

C．∠1＝∠2 D．无法确定

二 垂线的性质

活动2：

(1)用三角尺或量角器画已知直线l的垂线，这样的垂线能画几条？

(2)经过直线l上一点A画l的垂线，这样的垂线能画几条？

(3)经过直线l外一点B画l的垂点，这样的垂线能画几条？

展示点评：一条直线有无数条垂线，但经过一点(不论是点在直线上或是直线外)只能画一条已知直线的垂线．

小组讨论：过一点画已知直线的垂线有什么性质？

反思小结：在同一平面内过一点有且只有一条直线与已知直线垂直．过一点画已知直线的垂线，应分清是过直线上一点，还是过直线外一点画已知直线的垂线．画线段或射线的垂线，就是画它们所在直线的垂线．

针对训练

3．见教材第5页练习第2题．

4．画一条线段的垂线，垂足在( D )

A．这条线段上 B．这条线段的端点上

C．这条线段的延长线上 D．以上都可以

四、总结梳理　内化目标

回顾本节课学习内容，请回答下列问题：

1．谈谈你对垂线的认识．

2．垂线的性质是什么？为什么这一性质要加上前提“在同一平面内”？

五、达标检测 反思目标

1．如图，OA⊥OB，OD⊥OC，O为垂足，若∠AOC＝35°，则∠BOD＝__145°__．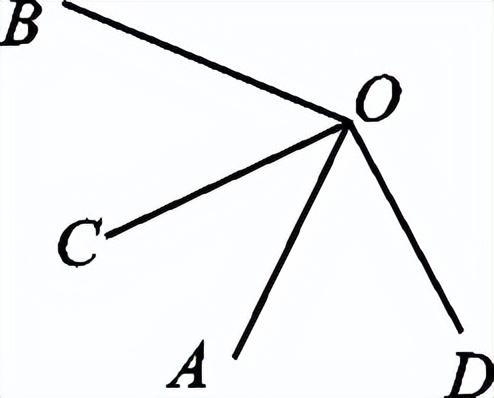

第1题图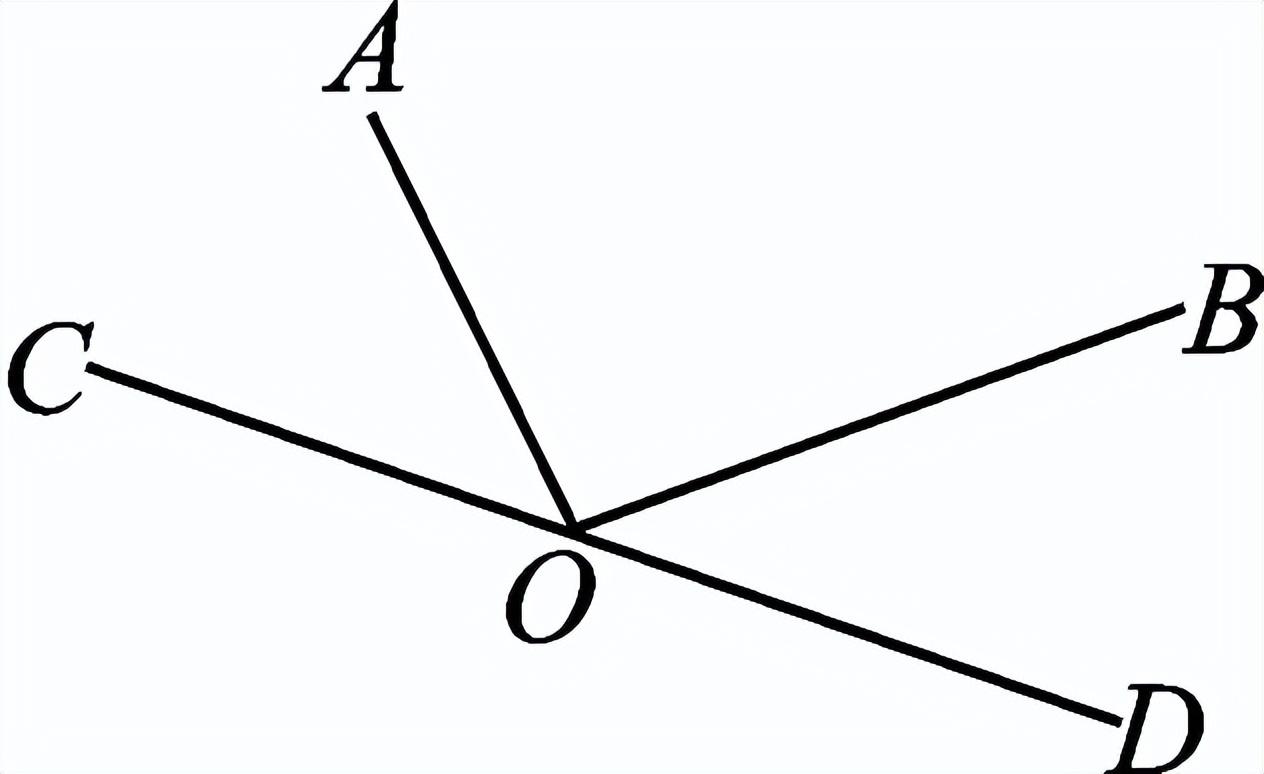

第2题图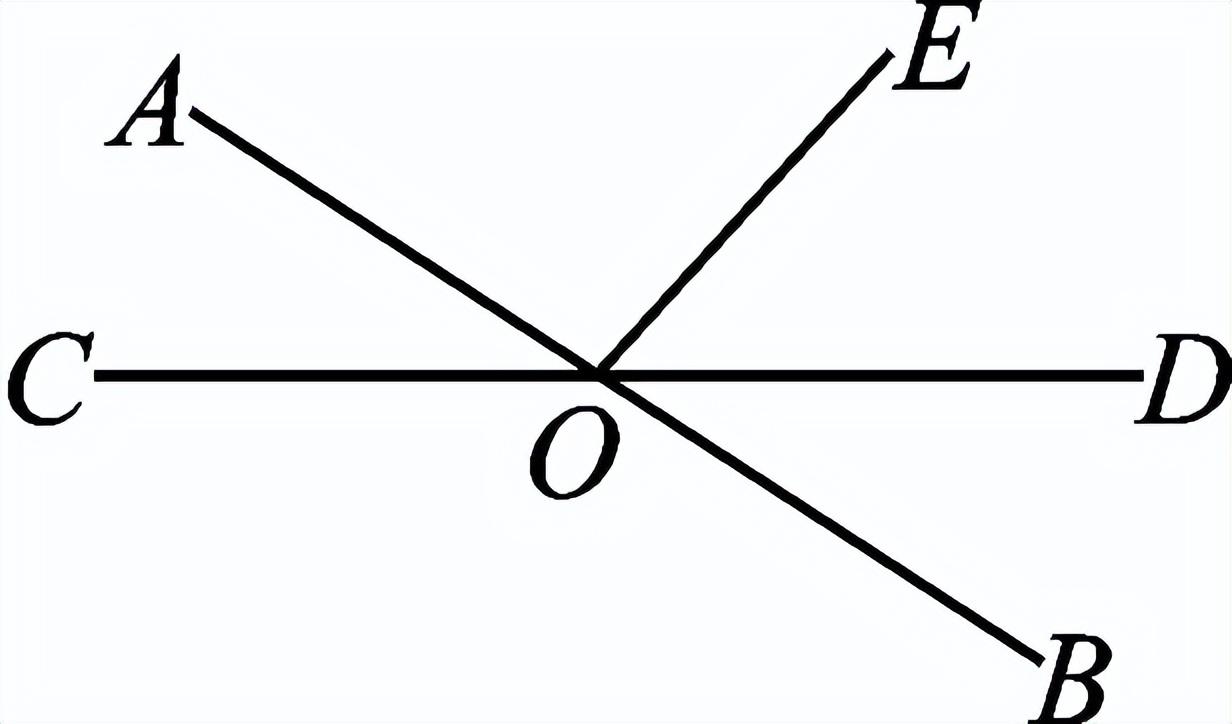 　　　

第3题图

2．如图，AO⊥BO，O为垂足，直线CD过点O，且∠BOD＝2∠AOC，则∠BOD＝__60°__．

3．如图，直线AB、CD相交于点O，若∠EOD＝40°，∠BOC＝130°，那么射线OE与直线AB的位置关系是__AB⊥OE__．

4．如图，直线AB，垂线OC交于点O，OD平分∠BOC，OE平分∠AOC.试判断OD与OE的位置关系．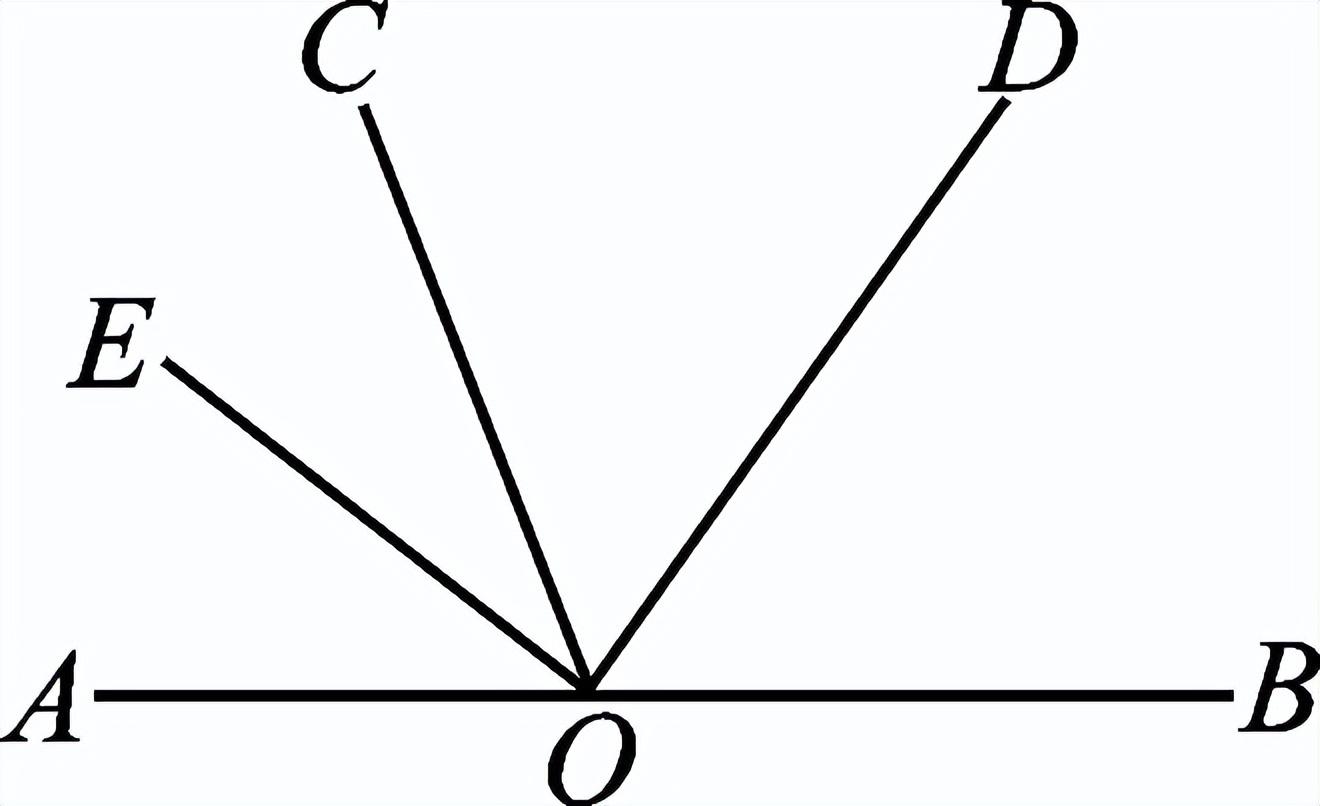

解：OD⊥OE

作业布置

(一)上交作业　教材第8至9页第4、5、12题．

(二)课后作业见学生用书．

修改补备

板

书

设

计

课

后

反

思