从无理数的定义和证明说开去
一:无理数定义
先来看无理数的定义,无理数是实数中不能精确地表示为两个整数之比的数,即无限不循环小数。
换句话说,无理数应满足三个条件:
①是小数;
②是无限小数;
③不循环.
二:相关数学史
我们所说的小数,是且只能是十进制小数。
①十进制,公元前14世纪中国商朝的记载中便已出现。公元10世纪传入欧洲,最早出现于西班牙的一份手稿。
②小数,公元前某个世纪便开始有了1/10,1/100的计量单位,公元5年的某份手稿中,便出现了9.5这样的数字。公 元14世纪传入阿拉伯,再经由阿拉伯,在公元16世纪传入欧洲。
③0这个数字古希腊也是没有的,是在公元8/9世纪由印度传入阿拉伯和欧洲的
三:古希腊无理数传说分析
那么我们来看看古希腊的希帕索斯是否能够判断出√2为无理数。根据勾股定理,对了,古希腊叫毕达哥拉斯定理,
是希帕索斯的老师的定理,所以希帕索斯一定知道直角边长为1的等腰直角三角形的斜边长是√2,但他能怎么证明√ 2是无理数呢?
①古希腊没有小数。。。。
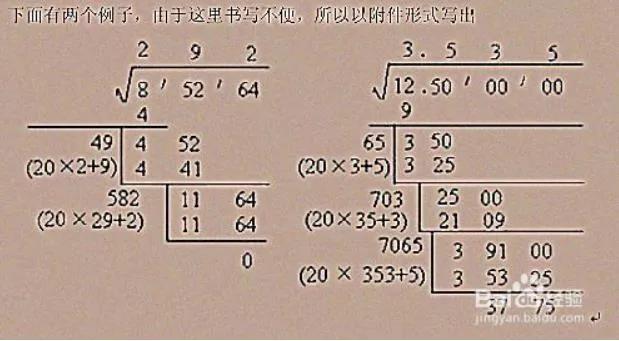
②不管了,楞开根号。那么填‘0’和十进制为基础的计算是无法避免的。参见附图开根号的过程。杯具的是,这两条也不能用,原因见二相关数学史
结论,希帕索斯的无理数咋证明的?还为此葬身鱼腹。。。。。编出这个故事的人更应该葬身鱼腹。推而广之,整个古希腊的数学也是咋看咋可疑